Излучение ЭМВ диполем
1. Уравнение ЭМВ. Этот частный случай излучения ЭМВ представляет значительный интерес, так как подобно диполю излучают атомы и молекулы, а также антенны (проводники с переменным током). Напомним, что под диполем понимают электронейтральную систему, состоящую из двух близко расположенных разноименных зарядов. Диполь характеризуется дипольным моментом Для того, чтобы заставить диполь излучать ЭМВ, необходимо создать ускоренное движение его зарядов. Для этого будем считать, что заряд (-q) совершает около неподвижного положительного заряда (+ q) вдоль оси диполя гармонические колебания с циклической частотой
где амплитуда вектора
В выражении (6.63) q – модуль одного из зарядов диполя, a – амплитуда ускорения, с которым движется отрицательный заряд ( Формула (6.63) справедлива в волновой зоне. Это область пространства, где максимальное значение вектора Удобно поверхность сферической волны разбить на параллели и меридианы по аналогии с поверхностью земного шара. Тогда из рис. 6.19, б следует, что
Рис. 6.19
вектор 2. Диаграмма направленности излучения диполя. Эта диаграмма показывает распределение энергии излучения по всем направлениям в пространстве. На ней откладываются отрезки прямой, длина которых пропорциональна интенсивности ЭМВ, излучаемой в данном направлении. Для диполя
где Из формулы (6.64) можно сделать следующие заключения: 1) диаграмма направленности излучения обладает осевой симметрией, так как интенсивность
Рис. 6.20 Применяя разные комбинации различных излучателей ЭМВ можно получить различные диаграммы направленности излучения. Так, например, узкую диаграмму направленности излучения - параллельный пучок ЭМВ можно получить, если поместить источник излучения в фокусе параболического зеркала (рис. 6.20, б), а самую широкую диаграмму направленности излучения - сферическую, дают три взаимно перпендикулярных диполя (рис. 6.20, в). 3.Мощность излучения ЭМВ. Открытый колебательный контур. В соответствии с формулой (6.63), мощность и интенсивность излучения диполя можно выразить следующим образом:
Итак, мощность и интенсивность излучаемой диполем электромагнитной волны прямо пропорциональны четвертой степени частоты колебаний его зарядов. Следовательно, увеличение частоты колебаний зарядов диполя приводит к резкому увеличению мощности излучаемых им ЭМВ. Поэтому выгодно передавать сигналы на большие расстояния с помощью ЭМВ высокой частоты. Для повышения циклической частоты собственных колебаний контура ( Он представляет собой отрезок проводника (антенну), в котором возбуждаются высокочастотные электромагнитные колебания. Они излучаются в пространство в виде ЭМВ большой мощности. Открытый колебательный контур также называют полуволновым диполем, так как на его длине укладывается половина длины волны, излучаемой антенной, или вибратором Герца. Отметим, что в антенне перекрываются электрическое и магнитное поля, это существенно повышает мощность излучения ЭМВ по сравнению с закрытым колебательным контуром. В связи с резким повышением мощности излучения высокочастотных колебаний передача сигнала звуковой частоты на большие расстояния происходит за счет модуляции ВЧ колебаний сигналом звуковой частоты. При
Рис. 6.21 приеме модулированного ВЧ сигнала проводят его детектирование, т.е. отделяют звуковой сигнал от высокочастотного колебания. Впервые ЭМВ экспериментально были обнаружены Герцем (1888 г.) с помощью открытого колебательного контура. Возбуждая в нем затухающие ВЧ колебания, он с помощью такого же приемного колебательного контура принимал ЭМВ и тем самым доказал факт их существования и подтвердил теорию Максвелла.
|

 , модуль которого равен произведению модуля одного из зарядов диполя на расстояние между ними (
, модуль которого равен произведению модуля одного из зарядов диполя на расстояние между ними ( ). Модуль напряженности электрического поля, создаваемого самим диполем, убывает с расстоянием от него по закону
). Модуль напряженности электрического поля, создаваемого самим диполем, убывает с расстоянием от него по закону  ~
~  .
. (рис. 6.19, а). Тогда расстояние между зарядами будет изменяться по закону
(рис. 6.19, а). Тогда расстояние между зарядами будет изменяться по закону  , а сам диполь, как это показывают расчеты, при
, а сам диполь, как это показывают расчеты, при  будет излучать сферическую ЭМВ, вектор напряженности электрического поля которой изменяется по закону
будет излучать сферическую ЭМВ, вектор напряженности электрического поля которой изменяется по закону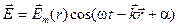 ,
, определяется формулой
определяется формулой ~
~ 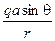 . (6.63)
. (6.63) ), угол θ – угол между осью диполя и вектором
), угол θ – угол между осью диполя и вектором  , проведенным от диполя в рассматриваемую точку пространства (рис. 6.19, б).
, проведенным от диполя в рассматриваемую точку пространства (рис. 6.19, б). ).
).
 располагается в плоскости, перпендикулярной к оси диполя, по касательной к параллели.
располагается в плоскости, перпендикулярной к оси диполя, по касательной к параллели.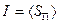 ~
~  ~
~  ,
, , (6.64)
, (6.64) – максимальная интенсивность излучаемых электромагнитных волн.
– максимальная интенсивность излучаемых электромагнитных волн. не зависит от угла
не зависит от угла  (рис. 6.20, в); 2) максимальная интенсивность излучения наблюдается по всем направлениям, лежащим в плоскости, перпендикулярной к оси диполя (
(рис. 6.20, в); 2) максимальная интенсивность излучения наблюдается по всем направлениям, лежащим в плоскости, перпендикулярной к оси диполя ( ); 3) вдоль оси диполь не излучает ЭМВ (
); 3) вдоль оси диполь не излучает ЭМВ ( ). Диаграмма направленности излучения диполя является достаточно широкой и, образно говоря, представляет собой бублик " без дырки".
). Диаграмма направленности излучения диполя является достаточно широкой и, образно говоря, представляет собой бублик " без дырки".
 ~
~  ~
~  ~
~  ~
~  ~
~  .
. ~
~ 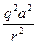
 ) необходимо уменьшать емкость С конденсатора (
) необходимо уменьшать емкость С конденсатора ( , т.е. уменьшать площадь его пластин и увеличивать расстояние между ними) и уменьшать индуктивность катушки (
, т.е. уменьшать площадь его пластин и увеличивать расстояние между ними) и уменьшать индуктивность катушки (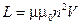 , т.е. уменьшать число ее витков). Это в итоге приводит к открытому колебательному контуру
, т.е. уменьшать число ее витков). Это в итоге приводит к открытому колебательному контуру 



