Свойства ЭМВ
Кратко рассмотрим основные свойства ЭМВ, которые можно получить из уравнений (6.37), (6.38), (6.40) и (6.41). Отметим, что эти свойства оказываются справедливыми и для других ЭМВ (сферических, цилиндрических и т.д.) 1. Скорость ЭМВ в вакууме не зависит от частоты и равна скорости света в вакууме (υ =с). Это свойство ЭМВ впервые позволило Максвеллу сделать вывод о том, что свет представляет собой электромагнитные волны определенного интервала частот. В среде скорость ЭМВ уменьшается и определяется характеристиками среды ε и μ. 2. Фазы колебаний векторов
Система уравнений должна иметь решения для любого момента времени и в любой точке пространства, что возможно только в том случае, если α 1=α 2, т.е. при совпадении фаз колебаний векторов
Рис. 6.13
3. ЭМВ является поперечной, так как колебания векторов 4. Плоская ЭМВ является линейно поляризованной, так как колебания вектора Для ЭМВ существуют и другие виды поляризаций (эллиптическая и круговая поляризации). Действительно, при распространении ЭМВ в анизотропной среде, свойства которой зависят от выбора направления в ней, разные составляющие вектора 5. Объемные плотности энергии электрического
Из-за совпадения фаз колебаний векторов
В соответствии с формулой (6.52) объемные плотности энергии электрического
и, следовательно, объемная плотность энергии ЭМВ запишется так
6. Вектор Пойнтинга или вектор плотности потока энергии (6.18) и (6.52) для вектора плотности потока энергии
Отметим, чтовектор плотности потока энергии для ЭМВ былвведен Пойнтингом и был назван в честь него. В связи с большой частотой ЭМВ многие приборы измеряют усредненные характеристики ЭМВ. Для них можно записать следующие формулы:
Усредненное по времени значение вектора Пойнтинга 7. ЭМВ могут поглощаться, отражаться и преломляться. 7. 1. Изменение фаз колебаний векторов при отражении. При отражении плоской ЭМВ от оптически более плотной среды ( Это означает, что при отражении падающей на границу раздела двух сред плоской электромагнитной волны тройка векторов
Рис. 6.14
Такое поведение векторов Для этого, в частном случае для угла падения
где в этих уравнениях взяты проекции векторов на направления, совпадающие с направлениями векторов
Решая систему уравнений (*), (***), получим
Так как модули векторов всегда больше нуля, то это означает, что Аналогично можно рассмотреть случай отражения ЭМВ от более плотной среды и получить формулы . 7. 2. Интенсивности падающей, отраженной и преломленной ЭМВ. Граничные условия также позволяют найти формулы, связывающие интенсивности падающей, отраженной и преломленной ЭМВ. Для этого необходимо использовать закон сохранения энергии, выполняющийся на границе раздела двух сред: энергия падающей на границу раздела двух сред электромагнитной волны будет равна сумме энергий, прошедшей во вторую среду ЭМВ и отраженной энергий. Тогда для векторов Пойнтинга падающей, преломленной и отраженной волн можно записать
При нормальном падении ЭМВ на границу раздела двух сред (угол падения
Введем коэффициент отражения R как отношение интенсивности волны, отраженной от границы раздела двух сред, к интенсивности волны, падающей на эту границу:
В случае нормального падения ЭМВ из уравнения (6.56, б) для случая
Для границы раздела воздух (
При переходе ЭМВ из одной среды в другую изменяются ее длина λ волны и скорость υ, а период Т волны и ее частота (ν) не изменяются (рис. 6.15, а):
где абсолютный показатель преломления среды n зависит от ε и μ, так как для многих сред μ =1, остается зависимость только от ε. 7. 3. Законы отражения и преломления. При падении плоской ЭМВ на границу раздела двух диэлектриков выполняются законы отражения и преломления (рис. 6.15). Закон отражения – падающий и отраженный лучи лежат в одной плоскости; угол падения равен углу отражения. Закон преломления – падающий и преломленный лучи лежат в одной плоскости; отношение синуса угла падения к синусу угла преломления равно отношению абсолютных показателей преломления второй среды к первой
где
Рис. 6.15
Отметим, что под лучом ЭМВ понимают направление распространения энергии ЭМВ, т.е. направление вектора Пойнтинга Законы отражения и преломления являются следствием граничных условий, накладываемых на нормальные и касательные составляющие векторов При переходе ЭМВ из оптически более плотной среды в оптически менее плотную среду может наблюдаться явление полного внутреннего отражения – явление, при котором падающая на границу раздела ЭМВ полностью
Рис. 6.16 отражается, не проникая во вторую среду (рис. 6.16). Это связано с тем, что при таком падении угол преломления всегда будет больше угла падения (r > i) и при увеличении угла падения наступает случай, при котором угол преломления станет равным
Явление полного внутреннего отражения используется в волоконной оптике, когда ЭМВ видимого диапазона излучения по оптическим волокнам передаются на большие расстояния без потери энергии. Такой способ передачи информации обладает большой пропускной способностью из-за высокой несущей частоты (для видимого диапазона излучения ω составляет порядка 3
|

 и
и  ЭМВ совпадают, т.е. в любой точке пространства вектора
ЭМВ совпадают, т.е. в любой точке пространства вектора  , (6.49)
, (6.49)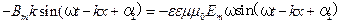 . (6.50)
. (6.50)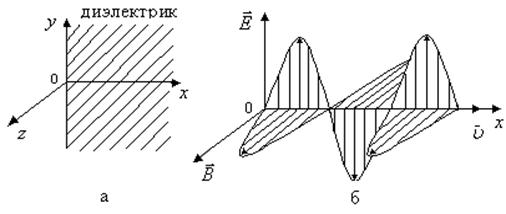
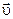 образуют жесткую тройку взаимно перпендикулярных векторов.
образуют жесткую тройку взаимно перпендикулярных векторов. , это приводит к эллиптической или круговой поляризации ЭМВ (конец вектора
, это приводит к эллиптической или круговой поляризации ЭМВ (конец вектора  и магнитного
и магнитного  полей ЭМВ одинаковы. Для того, чтобы показать это, запишем формулы взаимосвязи векторов
полей ЭМВ одинаковы. Для того, чтобы показать это, запишем формулы взаимосвязи векторов  . (6.51)
. (6.51)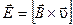 ,
,  . (6.52)
. (6.52) ,
, . (6.53)
. (6.53) . Из формул
. Из формул . (6.54)
. (6.54) ,
, . (6.55)
. (6.55) ) происходит изменение фазы колебаний вектора
) происходит изменение фазы колебаний вектора  (вектора
(вектора 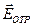 направлены в противоположные стороны, рис. 6.14, а). При этом изменение фазы вектора
направлены в противоположные стороны, рис. 6.14, а). При этом изменение фазы вектора 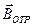 направлены в противоположные стороны, рис.6.14, а). При отражении от оптически менее плотной среды (
направлены в противоположные стороны, рис.6.14, а). При отражении от оптически менее плотной среды ( ) изменение фазы колебаний вектора
) изменение фазы колебаний вектора 
 , равного нулю:
, равного нулю:  , запишем граничные условия для касательных (тангенциальных, направленных параллельно поверхности границе раздела) составляющих векторов
, запишем граничные условия для касательных (тангенциальных, направленных параллельно поверхности границе раздела) составляющих векторов  :
: 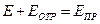 (*),
(*),  :
:  (**),
(**), , можно переписать уравнение (**) следующим образом:
, можно переписать уравнение (**) следующим образом: (***).
(***). ,
,  . (6.56, а)
. (6.56, а) ,
,  .
. ,
, 
 ,
, ,
, 
 . (6.57)
. (6.57) . (6.58)
. (6.58) =1) – стекло (
=1) – стекло ( =1, 5) значение коэффициента отражения R равно 0, 04, т.е. 4 % энергии ЭМВ в области диапазона видимого света теряется на отражение.
=1, 5) значение коэффициента отражения R равно 0, 04, т.е. 4 % энергии ЭМВ в области диапазона видимого света теряется на отражение. ,
,  ,
,  . (6.59)
. (6.59) ,
,  , (6.60)
, (6.60) называется абсолютным показателем преломления второй среды относительно первой.
называется абсолютным показателем преломления второй среды относительно первой.
 ,
,  ,
,  ,
,  и
и  (см. § 2.1.7 и § 4.3.3).
(см. § 2.1.7 и § 4.3.3).
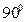 . Вводится предельный угол
. Вводится предельный угол  полного внутреннего отражения – это угол падения, при котором преломленный луч скользит по границе раздела двух сред, т.е. угол преломления равен
полного внутреннего отражения – это угол падения, при котором преломленный луч скользит по границе раздела двух сред, т.е. угол преломления равен  (см. рис. 6.16). Это позволяет записать условие для расчета этого угла для различных сред. Так, из уравнения (6.52) можно получить
(см. рис. 6.16). Это позволяет записать условие для расчета этого угла для различных сред. Так, из уравнения (6.52) можно получить . (6.61)
. (6.61) ) и большой защищенностью информации.
) и большой защищенностью информации.


