Уравнение Бернулли для реальной жидкости
Z1 +P1/rg+n2/2g=Z2+P2/rg+n22/2g+h1-2пот.=H (5.2)
Z +P/rg+n2/2g+h1-2пот.=Н (5.3) Реальная жидкость - это жидкость, в которой присутствует сила трения.
Геометрический смысл уравнения Бернулли:
Физический смысл уравнения Бернулли: При установившемся движении сумма четырех удельных энергий остается неизменной вдоль потока и равна полному запасу энергии. Z1 – энергия положения; P/rg – потенциальная энергия; n2/2g – кинетическая энергия; h1-2пот . – энергия, теряемая на пути от первого до второго сечения; Пьезометрическая линия соединяет уровни воды в пьезометрах. Падение этой линии называется пьезометрическим уклоном. Падение напорной линии на единицу длины называется гидравлическим уклоном. i= h1-2пот./L (5.4) L – длина участка; i – гидравлический уклон; h1-2пот . – это сумма потерь имеющаяся на данном участке;
h1-2пот.=åhдл.+åhмест. (5.5)
hдл. – потери по длине трубопровода; hмест. – местные потери (возникают при изменении конфигураций потока); Потери напора по длине определяются по формуле Дарси-Вейсбаха
hдл.=l(Lυ2/d2g) (5.6)
где l - коэффициент гидравлического сопротивления трения, коэффициент Дарси; L - длина трубопровода; d - внутренний диаметр; υ – скорость потока. Местные потери напора определяются по формуле Вейсбаха:
hмест.= åxυ2/2g (5.7)
x - коэффициент местных сопротивлений.
Лекция 6. Режимы движения жидкости
Существует два режима движения жидкости: 1. При ламинарном движении жидкость двигается струйками или слоями без взаимного перемешивания. 2. При турбулентном режиме происходит сильное перемешивание струек. При небольших скоростях жидкость двигается в ламинарном режиме, а затем переходит в турбулентный. Критерием для определения режима движения служит безразмерный параметр число Рейнольдса.
Re - число Рейнольдса;
Число Re, при котором происходит смена режимов, называется критическим. Re кр . =2320 - для напорного движения в трубопроводах. При Re кр . < 2320 – ламинарный режим При Re кр . > 2320 – турбулентный режим Re кр . =580 - безнапорное движение.
Скорость соответствующая Re кр называется критической скоростью.
Характеристика ламинарного режима Приламинарном режиме потока слои жидкости двигаются параллельно друг другу, скорости от стенок трубы к её оси нарастают плавно.
формула Пуазейля
|

 При установившемся движении жидкости сумма четырех высот в каждом живом сечении есть величина постоянная и равна полной высоте или полному напору.
При установившемся движении жидкости сумма четырех высот в каждом живом сечении есть величина постоянная и равна полной высоте или полному напору.
 h 1-2пот - потерянная высота (расстояние от первого до второго сечения движения воды)
h 1-2пот - потерянная высота (расстояние от первого до второго сечения движения воды)



 Н - полная высота или напор
Н - полная высота или напор (6.1)
(6.1) - кинематическая вязкость;
- кинематическая вязкость; (6.2)
(6.2)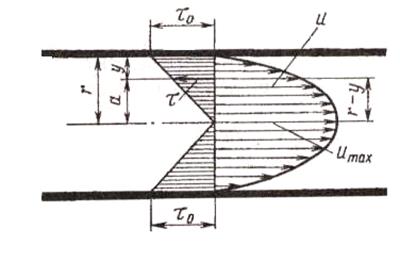
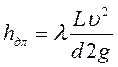
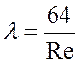 (6.3)
(6.3)


