Операторный метод расчета переходных процессов.
Определить: Решение.
1. Определим начальные условия:
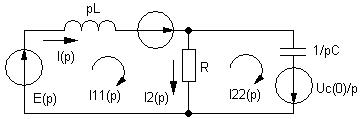
2. Составим операционную схему замещения для послекоммутационного периода времени:
Таким образом решение системы будет затруднено из-за её громоздкости, поэтому в данном случае лучше составить отдельную схему для свободной состовляющей. Общая запись системы уравнений остаётся неизменной, изменяется только конкретные значения
возьмём
Операторный метод расчета переходных процессов.
Недостаток классического метода – необходимость определения постоянных интегрирования, что сложно делать для цепей высокого порядка. В операторном методе не требуется определение постоянных интегрирования. В основе операторного метода лежит преобразование Лапласа. Суть использования преобразования состоит в следующем: решение из области действительного переменного t переводится в область комплексного переменного Функция f(t) называется оригиналом, F(p) – изображением. Переход от f(t) к F(p) называется прямым преобразованием. Переход от F(p) к f(t) называется обратным преобразованием. Часто преобразование Лапласа обозначается как
|

 Дано:
Дано:
 i2=f(t)
i2=f(t) ,
, ,
, ,
, ,
,  .
.
 ,
, ,
, ,
, ,
, ,
, ,
, .
. , а именно здесь отсутствует изображение
, а именно здесь отсутствует изображение  , то есть:
, то есть:  .
. ,
,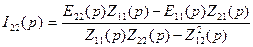 ,
,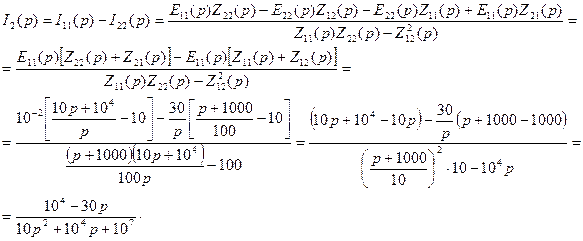 Этот же результат можно получить и методом двух узлов при начальных условиях
Этот же результат можно получить и методом двух узлов при начальных условиях  и
и  :
:

 .
. ,
, ,
, ,
, :
: ,
, ,
, 
 .
. . Комплексное число р называется оператором, при этом дифференциальные уравнения преобразуются в алгебраические. Проводится решение алгебраических уравнений, и затем осуществляется обратный переход в область действительного переменного t, т.е. находится решение, как функция времени.
. Комплексное число р называется оператором, при этом дифференциальные уравнения преобразуются в алгебраические. Проводится решение алгебраических уравнений, и затем осуществляется обратный переход в область действительного переменного t, т.е. находится решение, как функция времени. .
.


