п1. Функции и .
I. Описательные гипотезы: 1. Важной особенностью партийной системы России является отсутствие авторитетной и крупной стабильной партии, которая бы стала эффективным инструментом консолидации политических и экономических сил, элиты общества. 2. Роль авторитетной и крупной стабильной партии заменяет так называемая «партия власти», которая была создана ради обеспечения парламентской поддержки правительству и добивавшиеся определенного успеха на выборах при содействии главного властного центра – Президента и его администрации.
II. Объяснительные гипотезы: 1. Низкий рейтинг некоторых российских партий и невысокий уровень доверия к ним свидетельствует о низкой функциональности реально существующих партий по сравнению с представлениями российских граждан в ходе актуализации партийных идеологий; 2. Электоральный успех «партии власти» непосредственно зависит от рейтинга В.В. Путина.
III. Прогностические гипотезы: 1. Развитие института политических партий в России может привести к совершенному развитию гражданского общества и устоявшейся демократии в период электорального цикла; 2. Партийная конкуренция положительно влияет на общественно-политическую жизнь страны, потому что она способствует вовлечению граждан в переустройство страны. [1] Махрин А.В. Взаимозависимость партийной и избирательной систем в современной России: Монография. Тула: Изд-во ТулГУ, 2010. 188 с. [2] Берк Э. Правление, политика, общество. Сборник/Пер. с англ., сост., вступ., ст. и коммент.. Л.Полякова-М.: «КАНОН-ПРЕСС-Ц», «Кучково поле», 2001. – С.480. [3] Вебер М. Политика как призвание и профессия // Вебер М. Избранное. - М., 1990. – С. 670-687. [4] Benjamin Constant. Émile Faguet. [Электронный ресурс]. Режим доступа: http://fare.tunes.org/books/Faguet/benjamin_constant.html. [5] Лапаломбар Дж. и Вейнер М. Политические партии и политическое развитие. 1996 [6] Les partis politiques, P., 1951, 5 éd., P., 1964; (Дюверже М. Политические партии Пер. с франц. — М.:Академический Проект, 2000 538 с. Серия «Концепции». [7] GUNTER R., DIAMOND L. Species of political parties: A new tipology//Party politics – L. etc., 2003 – Vol. 9, N 2 – P. 167-199. [8] Гамбаров Ю.С. Политические партии в прошлом и настоящем. СПб., 1904. С.3-4 [9] Автономов А.С. Лоббизм и политические партии.//Представительная власть: мониторинг, анализ, информация, 1995, №3. С. 69-75 [10] Юдин Ю.А. Политические партии и право в современном государстве. М.: Издательская группа «Форум-ИНФРА-М», 1998. С.5, 37, 45, 47. [11] Лапаева В.В. Закон о политических партиях: вопросы взаимодействия партий с государством//журнал российского права. – М.: Норма, 2002, №4. – С.14-22. Теоретико—числовые функции. п1. Функции и. Определение. Целая часть Х — наибольшее целое число, не превосходящее х. Обозначение. [ x ]—целая часть х. Примеры.
Геометрический смысл: Замечание. Из определение целой часть следует, что Определение. Дробная часть х —разность между числом и его целой частью. Обозначение. Примеры.
Геометрический смысл: { x }—расстояние от [ x ] до x.
Замечание. Из определения дробных частей следует, что любое число х можно представить в виде суммы его целой и дробной частей: Наглядное представление о функциях
Заметим, что Свойства целой части. 1. Пусть Доказательство. Выпишем натуральные числа, которые делятся на n: Для любого положительного х верно неравенство Тогда ■ 2. Пусть Доказательство. Левая часть—количество натуральных чисел ■ 3. Для любых Доказательство. Складывая двойные неравенства ■ Пример. Следствие. Пусть Доказательство. Пусть Тогда Итак, указанное свойство действительно выражается записанной формулой. Но по свойству 2, ■ Примеры того как в теории чисел используется функция [ x ] будут приведены в п2. сейчас познакомимся с работой функции { x } на примере теоремы Дирихле. При доказательстве этой теоремы Дирихле впервые сформулировал принцип, который сейчас носит его имя. (“Если разместить Теорема (Дирихле). Пусть Иначе говоря: любое действительное число α; можно приблизить рационально с помощью дроби Доказательство. Рассмотрим t +1 число из промежутка [0;1): Разобьем [0;1) на t равных частей: По принципу Дирихле в одном из интервалов лежат 2 числа: Расстояние между ними меньше длины интервала: Далее, заменяя { x } на x –[ x ] получим
Обозначим
Значит, найдена рациональная дробь
■ Следствие. Для любого иррационального числа α множество чисел n α– m, где n и m — целые, всюду плотно на R, т.е. между любыми действительными х и у есть число вида n α – m. Иначе говоря: для любых
имеет целые решения n и m. Доказательство. Для любого, сколь угодно малого интервала (х; у) можно выбрать Для выбранного t, согласно теореме Дирихле, найдется рациональное число ■ Пример. Доказать, что существует квадрат целого числа, начинающийся с любой наперед заданной последовательности цифр Решение. Утверждение означает, что найдутся целые k и m такие, что После логарифмирования получим Пологая Существование целых n и m следует из следствий к теореме Дирихле. п.2 Каноническое разложение n!. Функции Чебышева. Согласно основной теореме арифметики Обозначение: Здесь Произведение Теорема 1. Показатель, с которым простое число р входит в произведение n! равен Замечание. Число слагаемых в формуле (которая представлена выше) конечно. Действительно, как только Доказательство. запишем произведение n! выделяя те сомножители, которые делятся на р:
Здесь kp — последнее число кратное р. По свойству 1 целой части Будем считать, что каждое из k выделенных чисел вносит по единице в итоговый показатель Итого, получим ■ Пример 1. найти наивысшую степень числа 7, на которую делится 900! Решение. Имеем n =900, p =7, поэтому Учитывая, что
Ответ:
Следствие. Пример 2. Найти каноническое разложение 16! Решение. Имеем
Ответ: Замечание. Пусть Тогда Формула (1) используется в различных теоретико-числовых соотношениях х. Пусть х —действительное число, Обозначение: Теорема 2. Показатель с которым простое число р входит в каноническое разложение К (х), равен Доказательство. пусть искомый показатель ■ Следствие. (При p > x все целые части равны нулю). Кратность Пример. Пусть х =10. проверим, что Произведение наименьших общих кратных в левой части равняется: С другой стороны ■ Тождество (3) было доказано Чебышевым в работах, посвященных исследованию распределения простых чисел (подробнее см. §4). Определение. Функциями Чебышева называют функции: Где суммы берутся по всем простым числам Замечание. При вычислении Пример. Непосредственно из определения следует, что Пример. Итак, Теорема 3. (Тождество Чебышева)
(Сумма в левой части конечна, т.к. Доказательство. Пусть С другой стороны, функция Тогда, суммируя эти функции по m, получим Так как условие для всех пар (K, m).
Замечание. Между функциями Сумма в правой части конечна: п.3 Мультипликативные функции. Определение. Функция f(x) определенная на множестве натуральных чисел, называется мультипликативной, если: 1)f(n) не равняется тождественно нулю; 2)для любых взаимно простых чисел n и m Пример. Функция В самом деле, В частности, функции Свойства мультипликативных функций. 1)Пусть f(x) мультипликативна. Тогда f(1)=1. Доказательство. Выберем ■ 2)произведение двух мультипликативных функций также является мультипликативной функцией. Доказательство. Пусть Для любых взаимно простых n и m. ■ 3)Пусть f(n) — мультипликативная функция; Доказательство. Поскольку Поэтому Продолжая тот же процесс получим требуемое. ■ 4)Пусть f(n) — мультипликативная функция, Доказательство. Следует из свойства 3. Замечание. Для того, чтобы построить мультипликативную функцию f (n) достаточно положить f (1)=1 и произвольно определить значения Действительно для взаимно простых n и m произведения f(nm) и f(n)f(m) будут состоять из одинаковых сомножителей, взятых, быть может, в другом порядке. Пример. Пусть f(1)=1, Тогда, например, Вообще говоря, если Опишем еще один способ построения мультипликативных функций. Обозначение: Пусть f(n) мультипликативна. Определим новую функцию: Пример. Если Теорема. Пусть f (n) мультипликативна, Тогда, Доказательство. Раскрывая скобки в правой части получим сумму слагаемых вида:
Где ■
|

 .
.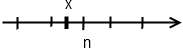
 — ближайшее целое число, слева от х.
— ближайшее целое число, слева от х. .
. —дробная часть х.
—дробная часть х.

 , где
, где 
 и
и  дают их графики:
дают их графики:

 ,
,  , где
, где 
 тогда
тогда  — количество натуральных чисел, которые не превосходят х и делится на n.
— количество натуральных чисел, которые не превосходят х и делится на n.
 при некотором
при некотором  .
.
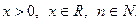 Тогда
Тогда 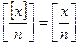
 и делящихся на n. Правая часть—количество натуральных чисел
и делящихся на n. Правая часть—количество натуральных чисел  и делящихся на n. Но между [ x ] и х нет других целых чисел, следовательно, указанные два числа равны.
и делящихся на n. Но между [ x ] и х нет других целых чисел, следовательно, указанные два числа равны.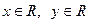
 или 1.
или 1. , получим
, получим  , это означает, что
, это означает, что  или
или  .
. . Но,
. Но, 
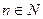 . Чтобы найти неполное частное от деления n на ab можно взять неполное частное от деления n на a и разделить его на b. Неполное частное от этого деления будет искомым:
. Чтобы найти неполное частное от деления n на ab можно взять неполное частное от деления n на a и разделить его на b. Неполное частное от этого деления будет искомым: 
 , где остаток
, где остаток 
 , где
, где  . Отсюда следует, что
. Отсюда следует, что  — неполное частное от деления n на а.
— неполное частное от деления n на а. .
. предмет в N ящиках, то хотя бы в одном ящике будет 2 перемета”).
предмет в N ящиках, то хотя бы в одном ящике будет 2 перемета”). Тогда существует рациональное число
Тогда существует рациональное число  такое, что
такое, что  , где
, где 
 ,
,  .
.
 .
. и
и  , можно считать, что
, можно считать, что 


 Число n и m — целые.
Число n и m — целые.
 двойное неравенство
двойное неравенство
 такое, что
такое, что  станет меньше, чем длинна интервала
станет меньше, чем длинна интервала  .
. такое, что
такое, что  располагается близко к нулю. Откладывая k раз отрезок длины
располагается близко к нулю. Откладывая k раз отрезок длины  , т.е.
, т.е.  .
. .
.
 .
. , получим
, получим 
 .
.
 — кратность, с которой простое число р входит в каноническое разложение n, т.е.
— кратность, с которой простое число р входит в каноническое разложение n, т.е.  — наибольший показатель, при котором n делится на
— наибольший показатель, при котором n делится на  (а на
(а на  число n уже не делится).
число n уже не делится). берется, вообще говоря, по всем простым р, но лишь конечное число показателей
берется, вообще говоря, по всем простым р, но лишь конечное число показателей  , так что это произведение не будет бесконечным.
, так что это произведение не будет бесконечным.
 станет больше, чем n, все целые части станут равны нулю.
станет больше, чем n, все целые части станут равны нулю.
 .
. . Но некоторые из выделенных чисел делятся на
. Но некоторые из выделенных чисел делятся на  и, значит, их вклад в показатель
и, значит, их вклад в показатель  . Затем,
. Затем,  чисел делятся на
чисел делятся на  , их вклад в общую сумму составит по 3 единицы и так далее.
, их вклад в общую сумму составит по 3 единицы и так далее. единиц составляющих в сумме показатель
единиц составляющих в сумме показатель  Все слагаемые, начиная с четвертого равны нулю, так как
Все слагаемые, начиная с четвертого равны нулю, так как  .
. ,
,  , вычисления удобно проводить по следующей схеме:
, вычисления удобно проводить по следующей схеме:

 .
.
 . При этом
. При этом 
 ,
,  ,
, 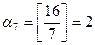 ,
,  ,
,  .
.
 ,
,  — наибольшая степень р, не превосходящая n.
— наибольшая степень р, не превосходящая n.
 .
.
 .
. . Тогда К (х) делится на
. Тогда К (х) делится на  . Это означает, что среди чисел 1, 2, 3, … [ x ] есть хотя бы одно число u, которое делится на
. Это означает, что среди чисел 1, 2, 3, … [ x ] есть хотя бы одно число u, которое делится на  . Логарифмируя неравенство, получим
. Логарифмируя неравенство, получим 

 !
!



 и по всем степеням простых чисел
и по всем степеням простых чисел  .
. , не превосходящим х.
, не превосходящим х.

 .
. , значит, логарифмируя тождество (3) получим следующее утверждение:
, значит, логарифмируя тождество (3) получим следующее утверждение:
 при х <2)
при х <2) . По теореме 1 и свойству 2 целой части
. По теореме 1 и свойству 2 целой части 
 можно записать в виде
можно записать в виде 

 для пар натуральных чисел (m, K) равносильно условию
для пар натуральных чисел (m, K) равносильно условию 

 , что следует из того, что
, что следует из того, что  .
. при х <2.
при х <2.
 мультипликативная при любых
мультипликативная при любых  .
.
 — мультипликативны.
— мультипликативны. так, что
так, что  . Тогда
. Тогда 
 , где f и g — мультипликативны. Тогда
, где f и g — мультипликативны. Тогда 
 — попарно взаимно простые числа. Тогда
— попарно взаимно простые числа. Тогда 
 при всех
при всех  , то
, то 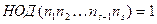

 — каноническое разложение числа n.
— каноническое разложение числа n. для всех простых р и всех
для всех простых р и всех  . Для остальных натуральных чисел значения f (n) вычисляются по формуле свойства 4.
. Для остальных натуральных чисел значения f (n) вычисляются по формуле свойства 4. при всех р и всех α.
при всех р и всех α.
 и
и  взаимно просты, то
взаимно просты, то  и
и  функция f (n) является мультипликативной.
функция f (n) является мультипликативной. — сумма по всем возможным делителям числа n.
— сумма по всем возможным делителям числа n.
 , то
, то  — сумма квадратов всех делителей числа n. Например,
— сумма квадратов всех делителей числа n. Например, 
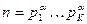 — каноническое разложение числа n.
— каноническое разложение числа n.

 . Число
. Число  является всевозможными делителями числа n (без пропусков и повторений). Следовательно, полученная сумма и есть
является всевозможными делителями числа n (без пропусков и повторений). Следовательно, полученная сумма и есть  .
.


