Формулы и уравнения. 6.7.1 Уравнения и формулы следует выделять из текста в отдельную строку посередине страницы
6.7.1 Уравнения и формулы следует выделять из текста в отдельную строку посередине страницы. Выше и ниже каждой формулы или уравнения должно быть оставлено не менее одной свободной строки. Если уравнение не умещается в одну строку, то оно должно быть перенесено после знака равенства (=) или после знаков плюс (+), минус (-), умножения (х), или других математических знаков, причем знак в начале следующей строки повторяют. При переносе формулы на знаке, символизирующем операцию умножения, применяют знак «Х». 6.7.2 Пояснение значений символов и числовых коэффициентов следует приводить непосредственно под формулой в той же последовательности, в которой они даны в формуле. Пояснения каждого символа следует давать с новой строки в той последовательности, в которой символы приведены в формуле. Первая строка пояснения должна начинаться со слова «где» без двоеточия после него. Пример – Плотность каждого образца ρ, кг/м3, вычисляют по формуле ρ; где m – масса образца, кг; V – объем образца, м3. Формулы, следующие одна за другой и не разделенные текстом, разделяются запятой. 6.7.3 Формулы следует нумеровать порядковой нумерацией в пределах всей работы арабскими цифрами в круглых скобках в крайнем правом положении на строке. Одну формулу обозначают – (1). Ссылки в тексте на порядковые номера формул дают в скобках, например, … в формуле (1). Формулы, помещаемые в приложениях, должны даваться отдельной нумерацией арабскими цифрами в пределах каждого приложения с добавлением перед каждой цифрой обозначения приложения, например, формула (В.1). Допускается нумерация формул в пределах раздела. В этом случае номер формулы состоит из номера раздела и порядкового номера формулы, разделенных точкой, например (3.1). 6.7.4 Порядок изложения математических уравнений такой же, как и формул. 6.7.5 Допускается выполнение формул и уравнений рукописным способом черными чернилами, высотой не менее 2,5 мм.
Ссылки 6.8.1 При ссылках на данную работу (проект) указывают номера разделов, подразделов, пунктов, подпунктов, перечислений, графического материала, формул, таблиц, приложений (в том числе на его разделы, подразделы, пункты, подпункты и таблицы), а также графы и строки таблиц данной работы (проекта) и позиции составных частей изделия на рисунке. При ссылках следует писать: «…в соответствии с разделом 2», «… согласно 3.1», «… по 3.1.1», «… в соответствии с рисунком А.2», «(рисунок 5)», «… по формуле (3)», «в соответствии с таблицей 1», «(таблица 4)», «… в соответствии с приложением А», «(приложение Г)» и т.п. При ссылках на структурную часть текста, имеющую нумерацию из цифр, не разделенных точкой, следует указывать наименование этой части полностью, например, «… в соответствии с разделом 5», «… по пункту 3», а при нумерации из цифр, разделенных точкой, наименование структурной части не указывают, например, «… по 4.10», «… в соответствии с 2.12». 6.8.2 Ссылки на использованные источники следует приводить в квадратных скобках.
|

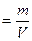
 , (1)
, (1)


