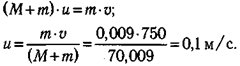F·dt 0→dp 0.

К процессам малой длительности относятся

• соударения движущихся тел

• распад тела на части (взрыв, выстрел, бросок).

Примеры

 

В боевиках часто присутствуют сцены, в которых после попадания пули человека отбрасывает по ходу выстрела. На экране это выглядит довольно эффектно. Проверим, возможно ли это? Пусть масса человек М =70 кг и он в момент попадания пули находится в состоянии покоя. Массу пули примем равной т = 9 г, а ее скорость v = 750 м/с. Если считать, что после попадания пули человек приходит в движение (в действительности этому может помешать сила трения между подошвами и полом), то для системы человек— пуля можно записать закон сохранения импульса: р ₁ = р_2. Перед попаданием пули человек не движется и в соответствии с (9.9) импульс системы р₁ = m∙v +0. Будем считать, что пуля застревает в теле. Тогда конечный импульс системы р ₂ = (М + т)∙и, где и — скорость, которую получил человек при попадании пули. Подставив эти выражения в закон сохранения импульса, получим:

 

Полученный результат показывает, что ни о каком отлетании человека на несколько метров не может быть и речи (кстати, тело, брошенное вверх со скоростью 0,1 м/с, поднимется на высоту всего 0,5 мм!).

2) Столкновение хоккеистов.

 

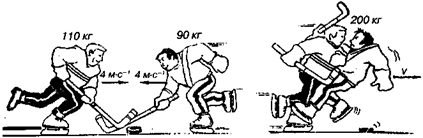
Два хоккеиста массой М₁ и М₂ двигаются навстречу друг другу со скоростями, соответственно, v_1, v₂ (рис. 9.12). Определить общую скорость их движения, считая столкновение абсолютно неупругим (при абсолютно неупругом ударе тела «сцепляются» и двигаются далее как одно целое).

Рис. 9.12. Абсолютно неупругое столкновение хоккеистов

 

Применим закон сохранения импульса к системе, состоящей из двух хоккеистов. Импульс системы перед столкновением p₁=M₁∙v₁ — M₂v_2. В этой формуле стоит знак «—» потому, что скорости v₁ и v₂ направлены навстречу друг другу. Направление скорости v₁ считается положительным, а направление скорости v₂ — отрицательным. После неупругого столкновения тела движутся с общей скоростью v и импульс системы р₂ = (M_l + M₂)∙v. Запишем закон сохранения импульса и найдем скорость v:

Направление скорости v определяется ее знаком.

Обратим внимание на одно важное обстоятельство: закон сохранения импульса можно применять только к свободным телам. Если движение одного из тел ограничено внешними связями, то общий импульс сохраняться не будет.