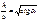РАСЧЕТ ЦЕНТРАЛЬНО СЖАТЫХ И ИЗГИБАЕМЫХ ДЕРЕВЯННЫХ ЭЛЕМЕНТОВ
РАСЧЕТ ЦЕНТРАЛЬНО СЖАТЫХ И ИЗГИБАЕМЫХ ДЕРЕВЯННЫХ ЭЛЕМЕНТОВ На сжатие работают стойки, подкосы, верхние пояса и отдельные стержни ферм (рис. 3.3).
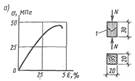
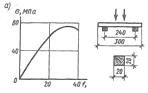
Рис. 3.3. Сжатый элемент: а — график деформаций и образец; б — схемы работы, разрушения и эпюра напряжений; в — типы закрепления концов и расчетные длины; г—график коэффициентов устойчивости φ в зависимости от гибкости λ;. Разрушение центрально сжатых элементов может произойти от потери устойчивости или прочности. Центрально сжатые элементы рассчитывают по формулам: - на прочность
- на устойчивость
где N – расчётное сжимающее усилие; F=(Fбр-Fосл), как для растянутых элементов; Fрасч – расчётная площадь поперечного сечения при проверке устойчивости. Принимается равной Fбр – при отсутствии ослаблений; при ослаблениях, не выходящих на кромку, если площадь ослаблений Fосл≤0,25Fбр, то Fрасч= Fбр; при Fосл>0,25 Fбр,
при симметричных ослаблениях, выходящих на кромки Fрасч= Fнт. При несимметричных ослаблениях, выходящих на кромку, элементы рассчитываются как внецентренно сжатые. Коэффициент продольного изгиба φ – отношение критического напряжения, при котором стержень теряет устойчивость, к пределу прочности материала на сжатие.
Коэффициент φ обычно меньше 1, зависит от гибкости стержня λ. При λ>λmin, коэффициент φ находится по формуле Эйлера:
Гибкость элементов λ определяют в зависимости от их расчётной длины и радиуса инерции поперечного сечения по формуле:
Расчётная длина зависит от способа закрепления элемента и равна На изгиб работают настилы, обрешётки, обшивки плит и панелей, стропильные ноги, прогоны, балки (рис. 3.4).
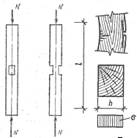
Рис. 3.4. Изгибаемый элемент: а — график прогибов и образец; б — схема работы и эпюры изгибающих моментов; в — схема разрушения и эпюры нормальных напряжений; г — схема работы при косом изгибе и эпюра напряжений Изгибаемые элементы рассчитываются на прочность и жёсткость (по деформациям или прогибам), т.е. по двум предельным состояниям. Различают два вида работы элементов на изгиб: простой изгиб, когда нагрузка действует в плоскости одной из главных осей инерции поперечного сечения элемента; косой изгиб, когда направление нагрузки не совпадает ни с одной из главных осей инерции сечения (рис. 3.4, б). Изгибаемые элементы на прочность при простом изгибе рассчитываются по формуле:
где Wрасч – расчётный момент сопротивления по площади нетто. Для клееных (гнутых) деревянных элементов Wрасч=Wнтmб(mгн), для составных стержней на податливых связях Wрасч=Wнтkw, При простом изгибе сечение по заданному изгибающему моменту М подбираются по формуле:
По найденному моменту сопротивления находят размеры поперечного сечения и подбирают пиломатериал по сортаменту, например для прямоугольного сечения.
При косом изгибе (рис. 3.4, г) расчёт элементов на прочность по нормальным напряжениям производится по формуле:
Мх и Мy – составляющие расчётного изгибающего момента относительно главных осей x и y, Wx и Wy – расчётные моменты сопротивления поперечного сечения нетто для осей х и y, Ru – расчётное сопротивление изгибу. Для подбора прямоугольного сечения косоизгибаемого элемента можно пользоваться формулами:
Проверка на скалывание производится по формуле Журавского:
Прогибы вычисляются как относительная величина
Прогиб элементов с учётом воздействия касательных напряжений определяют по формуле:
f0- прогиб без учёта касательных напряжений; k - коэффициент, зависящий от схемы нагружения внешней нагрузкой; β- коэффициент, зависящий от формы поперечного сечения и коэффициента Пуассона (μ) материала балки. Полный пролёт балки при косом изгибе равен геометрической сумме прогибов
Косой изгиб существенно увеличивает размеры прямоугольного сечения (прогонов), поэтому следует конструктивными мероприятиями добиваться того, чтобы основная нагрузка действовала в плоскости наибольшей жёсткости. Наименьшая площадь поперечного сечения прямоугольного прогона при косом изгибе из условия прочности получается при соблюдении отношения:
а из условия прогиба при
|






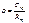
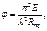

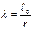

 .
.



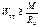



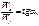

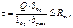
 в предположении упругой работы древесины по формулам сопротивления материалов в соответствии с расчётными схемами. Необходимо выполнение условия:
в предположении упругой работы древесины по формулам сопротивления материалов в соответствии с расчётными схемами. Необходимо выполнение условия:

 и
и  от составляющих сил
от составляющих сил  и
и