Решение краевой задачи для линейного
На сегодняшний день наиболее востребованными процедурами являются: лазерное омоложение кожи (принцип один – названий много: лазерная шлифовка, лазерная абляция, фракционный фототермолиз, фракционный термолиз, аблятивный фототермолиз, лазерная ревитализация, лазерная наноперфорация, дермальный оптический термолиз – иными словами структурное омоложение и устранение недостатков кожи лица и тела посредством лазерного излучения с различной геометрией проникновения) и эпиляция. Пациенты все больше доверяют лазерным технологиям и с каждым годом увеличивается число людей, которые предпочитают проходить лечение на лазерных аппаратах. Процедуры не инвазивны и подхватить какую-либо инфекцию просто невозможно. Они комфортны и безболезненны. В руках профессионала – безопасны. А эффективность давно не ограничивается только лишь косметологией – успешное лечение кожных заболеваний, реабилитационно-восстановительное лечение после пластических операций и клинические исследования продолжаются. Появляется много «доступных» и «бюджетных» новинок, обещающих чудо. Причем большинство из них «самые современные, безопасные и революционно эффективные». Уже есть модные «нано-«, загадочные «квантовые», скоро, видимо, придет очередь «на основе холодного ядерного синтеза» и «магнито-нуклеарных». Но сколько ВАЗ не модернизируй, «Мерседес» не получишь. Только производитель, вкладывающий очень много в научные исследования, отрабатывающий технологии в лабораториях, сотрудничающий с практикующими врачами разных стран и континентов будет делать эффективное и безопасное медицинское оборудование. А это не дешево. Либо ходите пешком – выбор за Вами. Это во-первых. Далее прослеживаются еще две тенденции – более селективное и прицельное воздействие либо одновременное комбинированное и интенсивное, несколько в одном. На мой взгляд, интенсивная комбинация и попытка достигнуть быстрого и многогранного эффекта далеко небезопасна, о чем уже говорят яркие и известные примеры. Кожа не броня, а организм не танк, и эстетическая медицина не поле боя. Любое внешнее воздействие организм должен принять, адаптироваться к нему и перейти на иное качественное состояние, комфортное и безопасное для его хозяина. Поэтому будущее за мягкими селективными технологиями, допускающие гармоничные комбинации не более двух отдельных методик. Остерегайтесь «чудес» и «революций».
Решение краевой задачи для линейного дифференциального уравнения второго порядка Пусть на отрезке
удовлетворяющее следующим краевым условиям:
Численное решение задачи состоит в нахождении приближенных значений
После соответствующих преобразований будем иметь
где
Полученная система имеет Решая уравнение (3) относительно
Предположим, что из этого уравнения исключена неизвестная
где Отсюда
Сравнивая формулы (4) и (5), получим для определения
Определим
Из формулы (4) при
Поэтому
На основании формул (6) и (7) последовательно определяются коэффициенты
получим
и по формуле (4) последовательно находим Для простейших краевых условий Отсюда
|

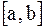 требуется найти решение дифференциального уравнения:
требуется найти решение дифференциального уравнения: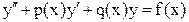 , (1)
, (1)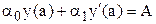 ;
;
 ;
;
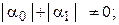

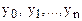 искомого решения
искомого решения 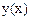 в точках
в точках 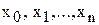 . Для этого разобьем отрезок
. Для этого разобьем отрезок 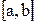 на
на 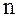 равных частей с шагом
равных частей с шагом  . Полагая
. Полагая 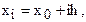
 и вводя обозначения
и вводя обозначения 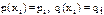 ,
, 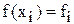 ,
, 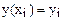 для внутренних точек
для внутренних точек  отрезка
отрезка 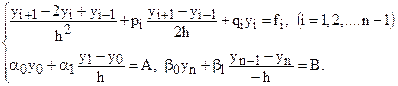
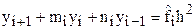 ,
, 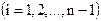 , (3)
, (3)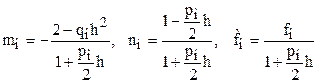 .
. линейных уравнений с
линейных уравнений с  , будем иметь
, будем иметь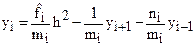 .
.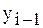 . Тогда это уравнение примет вид
. Тогда это уравнение примет вид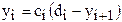 , (4)
, (4)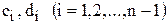 – некоторые коэффициенты.
– некоторые коэффициенты.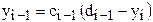 . Подставляя это выражение в (3), получим
. Подставляя это выражение в (3), получим 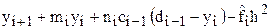 и, следовательно,
и, следовательно,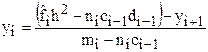 . (5)
. (5)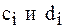 рекуррентные формулы:
рекуррентные формулы: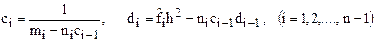 .
.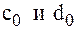 :
: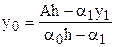 .
.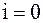 имеем
имеем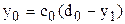 . (6)
. (6)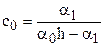 ,
, 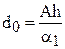 . (7)
. (7)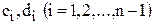 до
до 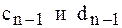 включительно (прямой ход). Обратный ход начинается с определения
включительно (прямой ход). Обратный ход начинается с определения 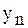 . Решая систему
. Решая систему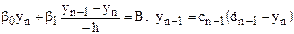 ,
,
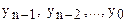 .
.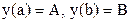 формулы для
формулы для 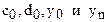 упрощаются. Полагая
упрощаются. Полагая  получим
получим 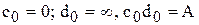 .
.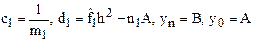 .
.


