Ответ: . Матричный метод решения систем линейных уравнений.

В этой статье поговорим о матричном методе решения систем линейных алгебраических уравнений вида , которые в матричной форме записываются как , где - основная матрица системы, - матрица-столбец неизвестных переменных, - матрица свободных членов.

Сначала опишем суть матричного метода, остановимся на условии применимости этого метода, далее подробно разберем решения нескольких примеров.

Сразу оговоримся, что решение систем линейных алгебраических уравнений матричным методом и решение СЛАУ с помощью обратной матрицы есть одно и то же. Поэтому рекомендуем освежить в памяти теорию раздела обратная матрица: определение, свойства, методы нахождения.

Приступим.

Пусть для матрицы А порядка n на n существует обратная матрица . Умножим обе части матричного уравнения слева на (порядки матриц A ⋅ X и В позволяют произвести такую операцию, смотрите статью операции над матрицами, свойства операций). Имеем . Так как для операции умножения матриц подходящих порядков характерно свойство ассоциативности, то последнее равенство можно переписать как , а по определению обратной матрицы 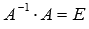(E – единичная матрица порядка n на n), поэтому

Таким образом, решение системы линейных алгебраических уравнений по матричному методу определяется равенством . Другими словами, решение СЛАУ находится с помощью обратной матрицы .

Мы знаем, что квадратная матрица А порядка n на n имеет обратную матрицу только тогда, когда ее определитель не равен нулю. Следовательно, СИСТЕМУ n ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ МОЖНО РЕШАТЬ МАТРИЧНЫМ МЕТОДОМ ТОЛЬКО ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ ОСНОВНОЙ МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ НУЛЯ.

Рассмотрим матричный метод на примерах. В некоторых примерах мы не будем подробно описывать процесс вычисления определителей матриц, при необходимости обращайтесь к статье вычисление определителя матрицы.