Лабораторная работа № 6. В пласте газ может залегать в условиях самых различных давлений и температур
В пласте газ может залегать в условиях самых различных давлений и температур. Для количественных определений и для изучения свойств газа в пластовых условиях нужно знать зависимости между объемом, давлением и температурой углеводородных газов. Эти соотношения для реальных газов значительно сложнее, чем для идеальных. Состояние идеальных газов выражается уравнением
РV = МRТ (6.1)
где р — давление газов в н/м2; V — объем, занимаемый газом при данном давлении, в м3; Т — абсолютная температура в град; М — масса газа в кг; R — газовая постоянная в дж/(кг-град). Причину и направление отклонений реальных газов от уравнения (1.21) можно установить, рассматривая основные исходные положения кинетической теории газов. Уравнение (1. 21) соответствует состоянию идеального газа, молекулы которого не взаимодействуют друг с другом. Молекулы же реальных газов обладают определенными размерами и взаимодействуют между собой. Реальный газ наиболее соответствует идеальному при низких давлениях. С повышением давления молекулы газа сближаются и силы притяжения между ними помогают внешним силам, сжимающим газ. Вследствие этого реальные газы сжимаются сильнее, чем идеальные, при тех же условиях. Когда реальный газ сильно сжат, межмолекулярные расстояния настолько уменьшаются, что отталкивающие силы начинают оказывать большие сопротивления дальнейшему уменьшению объема. В этих условиях реальный газ сжимается меньше, чем идеальный. Эти отклонения свойств реальных газов от свойств идеальных газов столь значительны, что на практике их нельзя не учитывать.
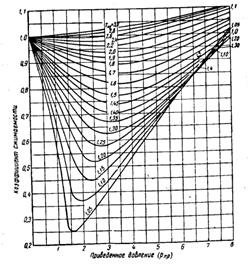
Рис. 7. Коэффициенты сжимаемости для нефтяного газа
Для определения степени отклонения сжимаемости реальных газов от идеальных пользуются коэффициентом сжимаемости Z, который показывает отношение объема реального газа к объему идеального газа при одних и тех же условиях. Тогда уравнение (1. 21) принимает вид:
pV = ZMRT. (6.2)
Для нефтяных газов значение коэффициента сжимаемости можно найти приближенно по кривым Брауна, приведенным на рис. 7. Коэффициент сжимаемости на этих кривых поставлен в зависимость от так называемых приведенного давления и приведенной температуры.
Приведенные давление и температура данного состава газа определяются по формулам
где р и Т — давление и температура газа; pкpi и Ткpi — критические давление и температура i-ro компонента;
уi — мольная концентрация i-ro компонента в газе.
Различные газы, имеющие одинаковые приведенные температуру и давление, находятся в «соответственных состояниях». По принципу соответственных состояний термодинамические свойства веществ (в том числе и коэффициенты сжимаемости различных газов), имеющих одинаковые приведенные температуры и давления, приблизительно одинаковы, так как при этом различные газы находятся как бы в одинаковом относительном приближении к жидкому состоянию. Поэтому графики коэффициента сжимаемости Z в приведенных координатах для углеводородов одного гомологического ряда совпадают с точностью, достаточной для практики. На этом основании график, приведенный на рис. 7, можно использовать для вычисления удельного объема и других параметров любого газа (в том числе и газовых смесей), если известны его критические параметры. Если известны объем газа Vo при нормальных условиях (р0 и То), то объем его при других давлениях и температурах (р и Т) можно найти, исходя из закона Гей-Люссака:
где То = 273°. Для перехода от объема в нормальных условиях к объему, занимаемому этим же количеством газа в пластовых условиях, служит объемный коэффициент. Численно он равен объему, который занял бы один кубический метр газа в пластовых условиях. Из уравнения (1. 24) объемный коэффициент газа будет
Вязкость газа. При низких давлениях вязкость газа не зависит от давления и возрастает с увеличением температуры. В пределах одного гомологического ряда углеводородов вязкость индивидуальных газов уменьшается с возрастанием молекулярной массы. Эти закономерности можно объяснить, исходя из кинетической теории газов, согласно которой зависимость динамической вязкости газа от его плотности, скорости молекул и длины их пробега определяется уравнением
где q — плотность газа; l — средняя длина свободного пути молекул; u — средняя скорость движения молекул. Из трех величин (ρ, λ и υ), входящих в уравнение (1. 26), скорость молекул не зависит от давления. Две же другие с увеличением давления изменяются в противоположных направлениях — плотность растет, а средняя длина свободного пробега молекул уменьшается. В итоге вязкость газа при низких давлениях (рис. 8) не зависит от изменения давления. Из уравнения (1.26) видно также, что с увеличением температуры вязкость при низких давлениях должна возрастать, так как при этом скорость движения молекул увеличивается. При увеличении давления вследствие уплотнения газа вязкость его с повышением температуры изменяется аналогично изменению вязкости жидкости – повышение температуры приводит к уменьшению вязкости газов (рис.8). Определение проницаемости пластов по данным исследования скважин на приток:
|

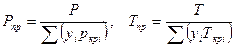 (6.3)
(6.3)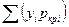
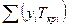 - среднекритические псевдокритические температура и давление;
- среднекритические псевдокритические температура и давление;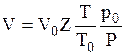 , (6.4)
, (6.4)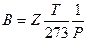 (6.5)
(6.5)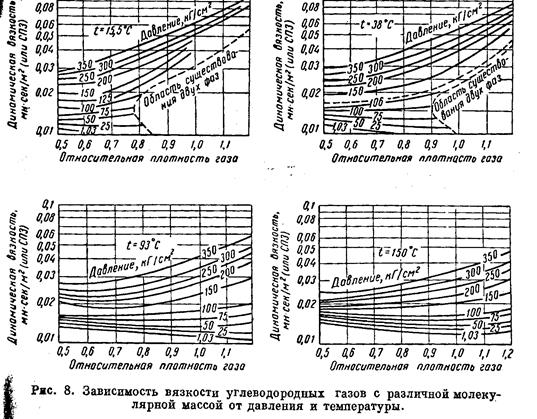
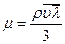 (6.6)
(6.6)


