Определение прогибов
4.31. Прогиб fm, обусловленный деформацией изгиба, определяется по формуле
где
Для изгибаемых элементов постоянного сечения без предварительного напряжения арматуры, имеющих трещины, на каждом участке, в пределах которого изгибающий момент не меняет знака, кривизну допускается вычислять для наиболее напряженного сечения, принимая ее для остальных сечений такого участка изменяющейся пропорционально значениям изгибающего момента (черт. 21).
Черт. 21. Эпюры изгибающих моментов и кривизны для железобетонных элементов постоянного сечения а ¾; схема расположения нагрузи; б ¾; эпюра изгибающих моментов; в — эпюра кривизны
4.32. Для изгибаемых элементов при 4.33. Прогиб fq, обусловленный деформацией сдвига, определяется по формуле
где g х — деформация сдвига, определяемая по формуле
здесь Qx — поперечная сила в сечении х от действия внешней нагрузки; G — модуль сдвига бетона (см. п. 2.16); jb 2 ¾ коэффициент, учитывающий влияние длительной ползучести бетона и принимаемый по табл. 34; jcrc ¾ коэффициент, учитывающий влияние трещин на деформации сдвига и принимаемый равным: на участках по длине элемента, где отсутствуют нормальные и наклонные к продольной оси элемента трещины, —1,0; на участках, где имеются только наклонные к продольной оси элемента трещины, — 4,8; на участках, где имеются только нормальные или нормальные и наклонные к продольной оси элемента трещины, — по формуле
где 4.34. Для сплошных плит толщиной менее 25 см (кроме опертых по контуру), армированных плоскими сетками, с трещинами в растянутой зоне значения прогибов, подсчитанные по формуле (171), умножаются на коэффициент 4.35. При расчете элементов с однорядным армированием (черт. 22) методом конечных элементов (или другими математическими методами) вместо уравнения (160) допускается использовать симметризированную систему физических зависимостей в виде:
где
e 0 — удлинения или укорочения вдоль оси у; Мact — момент внешних сил, расположенных по одну сторону рассматриваемого сечения, относительно оси y; Nact ¾; внешняя продольная сила, приложенная на уровне оси y и принимаемая при растяжении со знаком „плюс"; zs, zb — расстояния от оси у до точки приложения равнодействующей усилий соответственно в растянутой арматуре и в сжатом бетоне; x — определяется согласно указаниям п. 4.28; v — коэффициент, принимаемый по табл. 35; jf — коэффициент, определяемый по формуле (164) без учета арматуры, расположенной в сжатой зоне сечения; ys — определяется согласно указаниям п. 4.29; yb ¾; определяется согласно указаниям п. 4.27. Ось у располагается в пределах рабочей высоты сечения исходя из удобства расчетной схемы. Если ось у располагается выше центра тяжести площади сечения сжатой зоны, то величину zb следует принимать отрицательной.
Черт.22. Схема усилий и эпюра напряжений в сечении, нормальном к продольной оси элемента, с однорядным армированием при расчете по деформациям
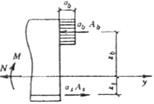
Для второго слагаемого в формуле (176) знак „минус" принимается, если усилие Р приложено ниже оси у, если усилие Р приложено выше оси y, то следует принимать знак „плюс". Для первого слагаемого в формуле (177) знак „плюс" принимается при растягивающем, а знак „минус" — при сжимающем усилии Nact. 4.36. При расчете элементов с многорядным расположением арматуры (черт. 23) рекомендуется использовать общую систему физических зависимостей вида:
где
i — порядковый номер стержня продольной растянутой арматуры; j — то же, сжатой арматуры; x 1 — относительная высота сжатой зоны сечения, равная jf — вычисляется по формуле (164) без учета арматуры S’; zsi, zsj — расстояния от центра тяжести i -й и j -й арматуры до оси y. В формуле (184) значения zsi, zsj, zb, принимаются положительными, если откладываются ниже оси y. В противном случае их следует принимать с отрицательным знаком.
Черт. 23. Схема усилий и эпюра напряжений в сечении, нормальном к продольной оси элемента, с многорядным армированием при расчете по деформациям
Значения x 1 и ysi для зависимостей (183) — (185) допускается определять согласно указаниям пп. 4.28 и 4.29, заменяя в расчетных формулах h 0 на h 01, Fa на
|

 (171)
(171) ¾ изгибающий момент в сечении х от действия единичной силы, приложенной по направлению искомого перемещения элемента в сечении х по длине пролета, для которого определяется прогиб;
¾ изгибающий момент в сечении х от действия единичной силы, приложенной по направлению искомого перемещения элемента в сечении х по длине пролета, для которого определяется прогиб; — полная кривизна элемента в сечении х от нагрузки, при которой определяется прогиб; значения
— полная кривизна элемента в сечении х от нагрузки, при которой определяется прогиб; значения  определяются по формулам (155) и (170) соответственно для участков без трещин и с трещинами; знак
определяются по формулам (155) и (170) соответственно для участков без трещин и с трещинами; знак 
 < 10 необходимо учитывать влияние поперечных сил на их прогиб. В этом случае полный прогиб ftot равен сумме прогибов, обусловленных соответственно деформацией изгиба fm и деформацией сдвига fq.
< 10 необходимо учитывать влияние поперечных сил на их прогиб. В этом случае полный прогиб ftot равен сумме прогибов, обусловленных соответственно деформацией изгиба fm и деформацией сдвига fq. (172)
(172) — поперечная сила в сечении х от действия по направлению искомого перемещения единичной силы, приложенной в сечении, где определяется прогиб;
— поперечная сила в сечении х от действия по направлению искомого перемещения единичной силы, приложенной в сечении, где определяется прогиб; (173)
(173) (174)
(174) —соответственно момент от внешней нагрузки и полная кривизна в сечении х от нагрузки, при которой определяется прогиб.
—соответственно момент от внешней нагрузки и полная кривизна в сечении х от нагрузки, при которой определяется прогиб.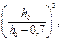 принимаемый не более 1,5, где h 0 — в см.
принимаемый не более 1,5, где h 0 — в см. (175)
(175) (176)
(176)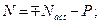 (177)
(177) (178)
(178) (179)
(179) (180)
(180) (181)
(181)
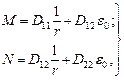 (182)
(182) (183)
(183)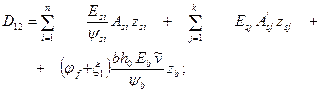 (184)
(184)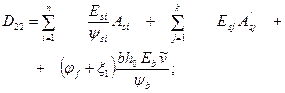 (185)
(185)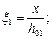

 (при определении m), jm на
(при определении m), jm на 



