Дифференцируемость неявных функций
Градиентом функции Обозначение:
Т.к.
С другой стороны:
Т.е. Следовательно,
Таким образом, градиент функции Лекция 27
Неявные функции, условие их существования. Дифференцируемость неявных функций
27.1.1. Неявная функция одного переменного: Уравнение Определим условия, когда уравнение (*) определяет переменную как функцию другой переменной.
Теорема 27.1 (о существовании неявной функции). Пустьфункция
Пример 27.1.
27.1.2. Неявная функция двух переменных:
Теорема 27.2. Пусть функция
Дифференцируемость неявных функций Если выполнены условия существования неявной функции, т.е. существует функция Тогда, дифференцируя как сложную функцию, имеем:
|
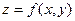в точке 
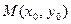называется вектор, компоненты которого равны 
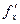и 
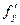, взятые в точке 
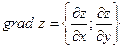(27.4)
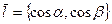, то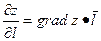
(27.5)
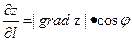(27.6)
максимально при 
(
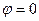), т.е.
.
(*)
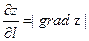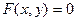. Если 
, 
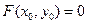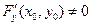, то уравнение (*) в окрестности точки 
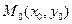имеет единственное непрерывное решение 
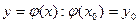, где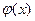 
непрерывно дифференцируема.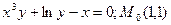
. т.е. существует функция 
(**)
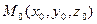. Если 
, 
, то уравнение (**) в окрестности точки 
имеет единственное решение 
, где 
имеет непрерывные частные производные.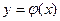
, то (*) имеет вид: 
.
.
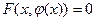