Лекция 27
Плоскость, проходящая через точку  поверхности, называется касательной плоскостью к поверхности в этой точке, если угол между секущей, проходящей через точку
поверхности, называется касательной плоскостью к поверхности в этой точке, если угол между секущей, проходящей через точку  и любой точкой
и любой точкой  этой плоскости стремится к нулю, когда
этой плоскости стремится к нулю, когда  .
.
Если  дифференцируема в точке
дифференцируема в точке  , то
, то
 (27.1)
(27.1)
– уравнение касательной плоскости к поверхности  в точке
в точке  .
.
В этом случае  – нормальный вектор касательной плоскости называют нормалью к поверхности
– нормальный вектор касательной плоскости называют нормалью к поверхности  и точке
и точке  , где
, где  .
.
Геометрический смысл.
 – угловой коэффициент касательной в точке
– угловой коэффициент касательной в точке  к сечению поверхности плоскостью
к сечению поверхности плоскостью  .
.
Частный дифференциал  – приращение аппликаты касательной плоскости.
– приращение аппликаты касательной плоскости.
Производная по направлению. Градиент.
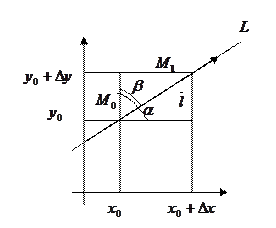
Пусть функция  определена в окрестности точки
определена в окрестности точки 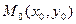 . Из точки
. Из точки  построим
построим  - произвольный единичный вектор (орт). Для характеристики скорости изменения функции в точке
- произвольный единичный вектор (орт). Для характеристики скорости изменения функции в точке  в направлении
в направлении  введем понятие производной по направлению.
введем понятие производной по направлению.
Через вектор  проведем прямую
проведем прямую  .
.
Выберем точку  в направлении вектора
в направлении вектора  . Тогда
. Тогда  .
.
В этом случае:
 .
.
Определение 27.2.
Если существует предел  , то он называется производной по направлению функции
, то он называется производной по направлению функции  в точке
в точке 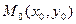 по направлению
по направлению  и обозначается
и обозначается  :
:
 (27.2)
(27.2)
Пусть функция  дифференцируема, тогда
дифференцируема, тогда
 .
.
Здесь  ,
, 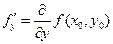
Разделив обе части равенства на  , и учитывая, что
, и учитывая, что
 ,
,
перейдем к пределу при  :
:
 (27.3)
(27.3)

 поверхности, называется касательной плоскостью к поверхности в этой точке, если угол между секущей, проходящей через точку
поверхности, называется касательной плоскостью к поверхности в этой точке, если угол между секущей, проходящей через точку  и любой точкой
и любой точкой  .
. дифференцируема в точке
дифференцируема в точке  , то
, то (27.1)
(27.1) в точке
в точке  .
. – нормальный вектор касательной плоскости называют нормалью к поверхности
– нормальный вектор касательной плоскости называют нормалью к поверхности  и точке
и точке  – угловой коэффициент касательной в точке
– угловой коэффициент касательной в точке  .
. – приращение аппликаты касательной плоскости.
– приращение аппликаты касательной плоскости.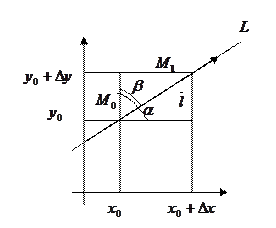
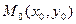 . Из точки
. Из точки  построим
построим  - произвольный единичный вектор (орт). Для характеристики скорости изменения функции в точке
- произвольный единичный вектор (орт). Для характеристики скорости изменения функции в точке  введем понятие производной по направлению.
введем понятие производной по направлению. .
. в направлении вектора
в направлении вектора  .
. .
. , то он называется производной по направлению функции
, то он называется производной по направлению функции  :
: (27.2)
(27.2) .
. ,
, 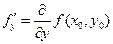
 , и учитывая, что
, и учитывая, что ,
, :
: (27.3)
(27.3)


