Центрально-растянутые и центрально-сжатые элементы
4.1. Расчет центрально-растянутых элементов следует производить по формуле где N - расчетная продольная сила; R p - расчетное сопротивление древесины растяжению вдоль волокон; F нт - площадь поперечного сечения элемента нетто. При определении F нт ослабления, расположенные на участке длиной до 200 мм, следует принимать совмещенными в одном сечении. 4.2. Расчет центрально-сжатых элементов постоянного цельного сечения следует производить по формулам: а) на прочность б) на устойчивость где R с - расчетное сопротивление древесины сжатию вдоль волокон; j - коэффициент продольного изгиба, определяемый согласно п. 4.3; F нт - площадь нетто поперечного сечения элемента; F рас - расчетная площадь поперечного сечения элемента, принимаемая равной: при отсутствии ослаблений или ослаблениях в опасных сечениях, не выходящих на кромки (рис. 1, а), если площадь ослаблений не превышает 25 % Е бр, Е расч = F бр, где F бр - площадь сечения брутто; при ослаблениях, не выходящих на кромки, если площадь ослабления превышает 25 % F бр, F рас = 4/3 F нт; при симметричных ослаблениях, выходящих на кромки (рис. 1, б), F рас = F нт.
Рис. 1. Ослабление сжатых элементов а -не выходящие на кромку; б - выходящие на кромку 4.3. Коэффициент продольного изгиба j следует определять по формулам (7) и (8); при гибкости элемента l £ 7 при гибкости элемента l > 70 где коэффициент а = 0,8 для древесины и а = 1 для фанеры; коэффициент А = 3000 для древесины и А = 2500 для фанеры. 4.4. Гибкость элементов цельного сечения определяют по формуле где l о - расчетная длина элемента; r - радиус инерции сечения элемента с максимальными размерами брутто соответственно относительно осей Х и У. 4.5. Расчетную длину элемента l о следует определять умножением его свободной длины l на коэффициент m0 l о = l m0 (10) согласно пп. 4.21 и 6.25. 4.6. Составные элементы на податливых соединениях, опертые всем сечением, следует рассчитывать на прочность и устойчивость по формулам (5) и (6), при этом F нт и F рас определять как суммарные площади всех ветвей. Гибкость составных элементов l следует определять с учетом податливости соединений по формуле где lу - гибкость всего элемента относительно оси У (рис. 2), вычисленная по расчетной длине элемента l о без учета податливости; l1 - гибкость отдельной ветви относительно оси I-I (см. рис. 2), вычисленная по расчетной длине ветви l 1; при l 1 меньше семи толщин (h 1) ветви принимаются l1 = 0; mу - коэффициент приведения гибкости, определяемый по формуле где b и h - ширина и высота поперечного сечения элемента, см: n ш - расчетное количество швов в элементе, определяемое числом швов, по которым суммируется взаимный сдвиг элементов (на рис. 2, а - 4 шва, на рис. 2, б - 5 швов); l о - расчетная длина элемента, м; n с - расчетное количество срезов связей в одном шве на 1 м элемента (при нескольких швах с различным количеством срезов следует принимать среднее для всех швов количество срезов); k с - коэффициент податливости соединений, который следует определять по формулам табл. 12. Таблица 12
Примечание. Диаметры гвоздей и нагелей d, толщину элементов а, ширину b пл и толщину d пластинчатых нагелей следует принимать в см.
Рис. 2. Составные элементы а - с прокладками; б - без прокладок При определении k с диаметр гвоздей следует принимать не более 0,1 толщины соединяемых элементов. Если размер защемленных концов гвоздей менее 4 d, то срезы в примыкающих к ним швах в расчете не учитывают. Значение k с соединений на стальных цилиндрических нагелях следует определять по толщине а более тонкого из соединяемых элементов. При определении k с диаметр дубовых цилиндрических нагелей следует принимать не более 0,25 толщины более тонкого из соединяемых элементов. Связи в швах следует расставлять равномерно по длине элемента. В шарнирно-опертых прямолинейных элементах допускается в средних четвертях длины ставить связи в половинном количестве, вводя в расчет по формуле (12) величину n с, принятую для крайних четвертей длины элемента. Гибкость составного элемента, вычисленную по формуле (11), следует принимать не более гибкости l отдельных ветвей, определяемой по формуле где å Ii бр - сумма моментов инерции брутто поперечных сечений отдельных ветвей относительно собственных осей, параллельных оси У (см. рис. 2); F бр - площадь сечения брутто элемента; l о - расчетная длина элемента. Гибкость составного элемента относительно оси, проходящей через центры тяжести сечений всех ветвей (ось Х на рис. 2), следует определять как для цельного элемента, т. е. без учета податливости связей, если ветви нагружены равномерно. В случае неравномерно нагруженных ветвей следует руководствоваться п. 4.7. Если ветви составного элемента имеют различное сечение, то расчетную гибкость l1 ветви в формуле (11) следует принимать равной: определение l 1 приведено на рис. 2. 4.7. Составные элементы на податливых соединениях, часть ветвей которых не оперта по концам, допускается рассчитывать на прочность и устойчивость по формулам (5), (6) при соблюдении следующих условий: а) площади поперечного сечения элемента F нт и F рас следует определять по сечению опертых ветвей; б) гибкость элемента относительно оси У (см. рис. 2) определяется по формуле (11); при этом момент инерции принимается с учетом всех ветвей, а площадь - только опертых; в) при определении гибкости относительно оси Х (см. рис. 2) момент инерции следует определять по формуле I = I о + 0,5 I но, (15) где I о и I но - моменты инерции поперечных сечений соответственно опертых и неопертых ветвей. 4.8. Расчет на устойчивость центрально-сжатых элементов переменного по высоте сечения следует выполнять по формуле где F макс - площадь поперечного сечения брутто с максимальными размерами; k ж N - коэффициент, учитывающий переменность высоты сечения, определяемый по табл. 1 прил. 4 (для элементов постоянного сечения k ж N = 1); j - коэффициент продольного изгиба, определяемый по п. 4.3 для гибкости, соответствующей сечению с максимальными размерами.
|

 , (4)
, (4) ; (5)
; (5) , (6)
, (6)
 ; (7)
; (7) , (8)
, (8) , (9)
, (9) , (11)
, (11)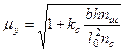 , (12)
, (12)
 , (13)
, (13) , (14)
, (14) , (16)
, (16)


