Интегрирование по частям обычно используется, если подынтегральная функция представляет произведение функций разных типов - степенная и показательная, степенная и тригонометрическая, обратная тригонометрическая функция и степенная, показательная и тригонометрическая и т.д. Интегрирование в этом случае производится с помощью формулы
 ,
,
где  функции одной переменной. При применении процедуры интегрирования по частям важен выбор функции
функции одной переменной. При применении процедуры интегрирования по частям важен выбор функции  .
.
Укажем приоритеты выбора этой функции.
1. В первую очередь в качестве  выбирается одна из функций
выбирается одна из функций 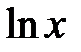 ,
, 
 .
.
2. При отсутствии этих функций в подынтегральном выражении в качестве  может быть выбрана находящаяся в числителе степенная функция с целым положительным показателем степени.
может быть выбрана находящаяся в числителе степенная функция с целым положительным показателем степени.
Других приоритетов при выборе этой функции нет, задание  в этом случае осуществляется перебором возможных вариантов.
в этом случае осуществляется перебором возможных вариантов.
Примеры.
1. 
 .
.
Билет
Практические вопросы
1. Производная
2. Предел
3. Производная по направлению
4.Производные функции одной или нескольких переменных
5. Неопределенный или определенный интеграл
6. Математическое ожидание или дисперсия дискретно заданной случайной величины
Теоретические вопросы
Методы Крамера или Гаусса.
Линии на плоскости. Прямая на плоскости и в пространстве, ее уравнения, кривые второго порядка.
Базис в 3-х мерном пространстве, представление вектора в базисе.
Пределы, их свойства.
Экстремумы функции одной переменной или наибольшее и наименьшее значения функции на отрезке
Асимптоты кривой или правило Лопиталя.
Формула Ньютона-Лейбница
Интегрирование НИ и ОИ по частям и заменой переменной.
Интегрирование простейших дробно рациональных функций.
Интегралы 
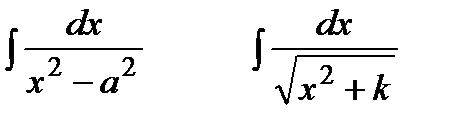 .
.
Представление правильной дробно рациональной функции в виде
суммы простейших дробей.
Универсальнапя тригонометрическая подстановка.
Замена  .
.
Основные формулы комбинаторики
Определения вероятности случайного события
Сумма или произведение случайных событий, их вероятность
Математическое ожидание, дисперсия, их свойства, среднее квадратическое отклонение.
Нормальный закон распределения, его параметры.
Генеральная и выборочная совокупности, их точечные и интервальные оценки.
Оценка генеральной совокупности по ее выборке. Смещенная и несмещенная оценки.
Доверительный интервал.
Коэффициент корреляции.
УМВД России по Калужской области
o
Начало формы
 ·
·  ·
·  ·
·  ·
·  ·
· 
|
| Главная → Новости
Юные инспекторы рассказали обнинским малышам о правилах дорожного движения
28 Февраля 12:20
 Сотрудниками ГИБДД ОМВД России по г.Обнинску уделяется особое внимание пропагандистской работе по профилактике детского дорожно-транспортного травматизма. В этом им помогают отряды юных инспекторов движения, которые уже на протяжении нескольких лет действуют во многих школах города.
27 февраля старшеклассники 11-й школы доказали, что тоже готовы стать помощниками сотрудников ГИБДД в этой важной и полезной работе. Ребята показали спектакль на тему дорожной безопасности воспитанникам детского сада «Россиянка». Когда-то сегодняшние учащиеся седьмых и восьмых классов сами ходили в этот детский садик рядом со своей школой, а теперь пришли в качестве гостей, чтобы поделиться своими знаниями правил дорожного движения. Ребята уверены, что изучать и соблюдать эти правила важно с самого раннего возраста.
Для того, чтобы наглядно показать зрителям, как вести себя на проезжей части, где и как можно переходить дорогу, школьники разучили песни, стихи, танцы и приготовили соответствующий реквизит. В спектакле был задействован настоящий инспектор ГИБДД с обязательными атрибутами: жезлом, фуражкой и светоотражающим жилетом. Демонстрировал навыки вождения велосипедист, а «Скорая помощь» оказывала помощь пострадавшим. На перекрестке подавал нужными сигналы светофор. В итоге все участники представления смогли наглядно получить урок безопасного поведения на дорогах.
Сами малыши тоже смогли принять участие в театральной постановке и продемонстрировать свои знания. На радость организаторам мероприятия, воспитателей и сотрудников полиции дети из «Россиянки» справились со всеми заданиями на «отлично». Малыши не только правильно называли знаки дорожного движения, но и читали стихи, а также заранее подготовили серию рисунков и плакатов по заданной тематике.
В завершение мероприятия инспектор ГИБДД ОМВД России по г.Обнинску Андрей Коленов поблагодарил организаторов и участников, которые внесли свой вклад в профилактическую работу по предупреждению детского дорожно-транспортного травматизма, и подарил малышам сладкие подарки, а также светоотражающие элементы и брелоки, которые делают маленьких участников дорожного движения заметнее на дорогах.
Пресс-служба ОМВД России по г.Обнинску
·
Сотрудниками ГИБДД ОМВД России по г.Обнинску уделяется особое внимание пропагандистской работе по профилактике детского дорожно-транспортного травматизма. В этом им помогают отряды юных инспекторов движения, которые уже на протяжении нескольких лет действуют во многих школах города.
27 февраля старшеклассники 11-й школы доказали, что тоже готовы стать помощниками сотрудников ГИБДД в этой важной и полезной работе. Ребята показали спектакль на тему дорожной безопасности воспитанникам детского сада «Россиянка». Когда-то сегодняшние учащиеся седьмых и восьмых классов сами ходили в этот детский садик рядом со своей школой, а теперь пришли в качестве гостей, чтобы поделиться своими знаниями правил дорожного движения. Ребята уверены, что изучать и соблюдать эти правила важно с самого раннего возраста.
Для того, чтобы наглядно показать зрителям, как вести себя на проезжей части, где и как можно переходить дорогу, школьники разучили песни, стихи, танцы и приготовили соответствующий реквизит. В спектакле был задействован настоящий инспектор ГИБДД с обязательными атрибутами: жезлом, фуражкой и светоотражающим жилетом. Демонстрировал навыки вождения велосипедист, а «Скорая помощь» оказывала помощь пострадавшим. На перекрестке подавал нужными сигналы светофор. В итоге все участники представления смогли наглядно получить урок безопасного поведения на дорогах.
Сами малыши тоже смогли принять участие в театральной постановке и продемонстрировать свои знания. На радость организаторам мероприятия, воспитателей и сотрудников полиции дети из «Россиянки» справились со всеми заданиями на «отлично». Малыши не только правильно называли знаки дорожного движения, но и читали стихи, а также заранее подготовили серию рисунков и плакатов по заданной тематике.
В завершение мероприятия инспектор ГИБДД ОМВД России по г.Обнинску Андрей Коленов поблагодарил организаторов и участников, которые внесли свой вклад в профилактическую работу по предупреждению детского дорожно-транспортного травматизма, и подарил малышам сладкие подарки, а также светоотражающие элементы и брелоки, которые делают маленьких участников дорожного движения заметнее на дорогах.
Пресс-служба ОМВД России по г.Обнинску
·  ·
· 
| |

 ,
, функции одной переменной. При применении процедуры интегрирования по частям важен выбор функции
функции одной переменной. При применении процедуры интегрирования по частям важен выбор функции  .
.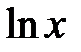 ,
, 
 .
. может быть выбрана находящаяся в числителе степенная функция с целым положительным показателем степени.
может быть выбрана находящаяся в числителе степенная функция с целым положительным показателем степени.
 .
.
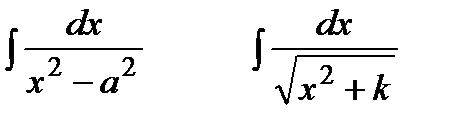 .
. .
. ·
·  ·
·  ·
·  ·
·  ·
· 
 Сотрудниками ГИБДД ОМВД России по г.Обнинску уделяется особое внимание пропагандистской работе по профилактике детского дорожно-транспортного травматизма. В этом им помогают отряды юных инспекторов движения, которые уже на протяжении нескольких лет действуют во многих школах города.
27 февраля старшеклассники 11-й школы доказали, что тоже готовы стать помощниками сотрудников ГИБДД в этой важной и полезной работе. Ребята показали спектакль на тему дорожной безопасности воспитанникам детского сада «Россиянка». Когда-то сегодняшние учащиеся седьмых и восьмых классов сами ходили в этот детский садик рядом со своей школой, а теперь пришли в качестве гостей, чтобы поделиться своими знаниями правил дорожного движения. Ребята уверены, что изучать и соблюдать эти правила важно с самого раннего возраста.
Для того, чтобы наглядно показать зрителям, как вести себя на проезжей части, где и как можно переходить дорогу, школьники разучили песни, стихи, танцы и приготовили соответствующий реквизит. В спектакле был задействован настоящий инспектор ГИБДД с обязательными атрибутами: жезлом, фуражкой и светоотражающим жилетом. Демонстрировал навыки вождения велосипедист, а «Скорая помощь» оказывала помощь пострадавшим. На перекрестке подавал нужными сигналы светофор. В итоге все участники представления смогли наглядно получить урок безопасного поведения на дорогах.
Сами малыши тоже смогли принять участие в театральной постановке и продемонстрировать свои знания. На радость организаторам мероприятия, воспитателей и сотрудников полиции дети из «Россиянки» справились со всеми заданиями на «отлично». Малыши не только правильно называли знаки дорожного движения, но и читали стихи, а также заранее подготовили серию рисунков и плакатов по заданной тематике.
В завершение мероприятия инспектор ГИБДД ОМВД России по г.Обнинску Андрей Коленов поблагодарил организаторов и участников, которые внесли свой вклад в профилактическую работу по предупреждению детского дорожно-транспортного травматизма, и подарил малышам сладкие подарки, а также светоотражающие элементы и брелоки, которые делают маленьких участников дорожного движения заметнее на дорогах.
Пресс-служба ОМВД России по г.Обнинску
·
Сотрудниками ГИБДД ОМВД России по г.Обнинску уделяется особое внимание пропагандистской работе по профилактике детского дорожно-транспортного травматизма. В этом им помогают отряды юных инспекторов движения, которые уже на протяжении нескольких лет действуют во многих школах города.
27 февраля старшеклассники 11-й школы доказали, что тоже готовы стать помощниками сотрудников ГИБДД в этой важной и полезной работе. Ребята показали спектакль на тему дорожной безопасности воспитанникам детского сада «Россиянка». Когда-то сегодняшние учащиеся седьмых и восьмых классов сами ходили в этот детский садик рядом со своей школой, а теперь пришли в качестве гостей, чтобы поделиться своими знаниями правил дорожного движения. Ребята уверены, что изучать и соблюдать эти правила важно с самого раннего возраста.
Для того, чтобы наглядно показать зрителям, как вести себя на проезжей части, где и как можно переходить дорогу, школьники разучили песни, стихи, танцы и приготовили соответствующий реквизит. В спектакле был задействован настоящий инспектор ГИБДД с обязательными атрибутами: жезлом, фуражкой и светоотражающим жилетом. Демонстрировал навыки вождения велосипедист, а «Скорая помощь» оказывала помощь пострадавшим. На перекрестке подавал нужными сигналы светофор. В итоге все участники представления смогли наглядно получить урок безопасного поведения на дорогах.
Сами малыши тоже смогли принять участие в театральной постановке и продемонстрировать свои знания. На радость организаторам мероприятия, воспитателей и сотрудников полиции дети из «Россиянки» справились со всеми заданиями на «отлично». Малыши не только правильно называли знаки дорожного движения, но и читали стихи, а также заранее подготовили серию рисунков и плакатов по заданной тематике.
В завершение мероприятия инспектор ГИБДД ОМВД России по г.Обнинску Андрей Коленов поблагодарил организаторов и участников, которые внесли свой вклад в профилактическую работу по предупреждению детского дорожно-транспортного травматизма, и подарил малышам сладкие подарки, а также светоотражающие элементы и брелоки, которые делают маленьких участников дорожного движения заметнее на дорогах.
Пресс-служба ОМВД России по г.Обнинску
·  ·
· 



