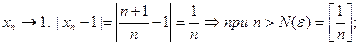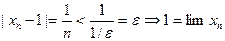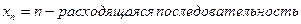Число а называется пределом последовательности xn для любого (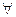 ) сколь угодно малого положительного числа
) сколь угодно малого положительного числа 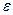 найдется номер, зависящий от
найдется номер, зависящий от 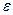 , начиная с которого все члены последовательности отличаются от а меньше, чем на
, начиная с которого все члены последовательности отличаются от а меньше, чем на 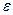 .
.
Предел последовательности
Под числовой последовательностью 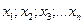 понимают функцию
понимают функцию 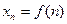 , заданную на множестве натуральных чисел
, заданную на множестве натуральных чисел 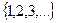 т.е. функцию натурального аргумента.
т.е. функцию натурального аргумента.
Число a называется пределом последовательности xn (x=1,2,…): 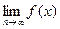 =а, если для любого сколь угодно малого
=а, если для любого сколь угодно малого 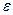 >0, существует такое число N=N(
>0, существует такое число N=N(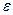 ), что для всех натуральных n>N выполняется неравенство
), что для всех натуральных n>N выполняется неравенство 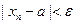 .
.
1) 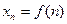 ,
, 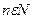 - натуральное число. Если xn=a, то (a, a, a, a) – стационарная последовательность.
- натуральное число. Если xn=a, то (a, a, a, a) – стационарная последовательность.
2)  , где a, d – const, тогда (a, a+d, a+2d,…a+(n-1)d)
, где a, d – const, тогда (a, a+d, a+2d,…a+(n-1)d)
xn+1=xn+d – рекуррентная формула.
3) Числа Фибоначчи. (1,1, 2, 3, 5, 8, 13, 21,…), где x1, x2 =1 и 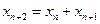 .
.
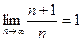 (*);
(*);
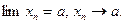
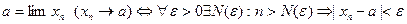
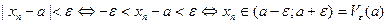 - эпсилон – окрестность числа а.
- эпсилон – окрестность числа а.
1.  .
. 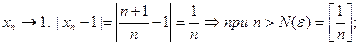
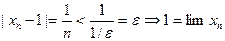
2. 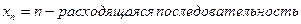
Основные теоремы пределах
- О единственном пределе. Последовательность имеет не более 1 предела.
- Предельный переход в неравенстве.
- О трех последовательностях. О сжатой последовательности.

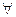 ) сколь угодно малого положительного числа
) сколь угодно малого положительного числа 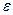 найдется номер, зависящий от
найдется номер, зависящий от 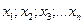 понимают функцию
понимают функцию 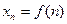 , заданную на множестве натуральных чисел
, заданную на множестве натуральных чисел 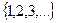 т.е. функцию натурального аргумента.
т.е. функцию натурального аргумента.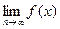 =а, если для любого сколь угодно малого
=а, если для любого сколь угодно малого 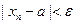 .
.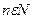 - натуральное число. Если xn=a, то (a, a, a, a) – стационарная последовательность.
- натуральное число. Если xn=a, то (a, a, a, a) – стационарная последовательность. , где a, d – const, тогда (a, a+d, a+2d,…a+(n-1)d)
, где a, d – const, тогда (a, a+d, a+2d,…a+(n-1)d)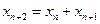 .
.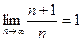 (*);
(*);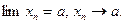
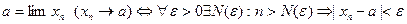
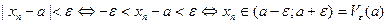 - эпсилон – окрестность числа а.
- эпсилон – окрестность числа а. .
.