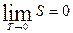Число различных микросостояний, соответствующих данному макросостоянию, называется статистическим весом, или термодинамической вероятностью.
Пример: как 4 молекулы могут распределяться между двумя половинками сосуда:
В общем случае число микросостояний, отвечающих макросостоянию
Вероятность макросостояния равна отношению его статистического веса к полному числу состояний. Отметим, что W не обладает свойство аддитивности. Если система, к примеру, состоит из двух подсистем, то W=W1 W2. Поэтому в качестве характеристики вероятности состояния принимается величина S=k lnW, которая называется энтропией. ü Энтропия изолированной системы возрастает, т.к. система переходит из менее вероятных в более вероятные состояния; ü Энтропия системы, находящейся в равновесном состоянии, максимальна. Первое утверждение носит название закона возрастания энтропии, или второго начала термодинамики. Состояние, осуществляемое относительно малым числом способов, называется упорядоченным или неслучайным. Таким образом, энтропия является мерой молекулярного беспорядка в системе. Соотношение При абсолютном нуле температуры всякое тело находится в основном состоянии, стат. вес которого равен единице т.е.
|
, (W(2,4-2)=6, W(1,4-1)=4)
(необр. процесс), означает, что сообщение системе тепла приводит к усилению теплового движения, и, следовательно, к увеличению степени беспорядка в системе.
