| № п/п
|
Понятие
|
Формулировка
|
Примечание
|
| 1.
| Определение функции
| Функцией называется зависимость переменной у от переменной х, при которой каждому значению х соответствует единственное значение у.
| у = f (x) или y=g(x)
x– независимая переменная (аргумент)
у – зависимая переменная (значение функции)
|
| 2.
| Область определения функции
| Все значения независимой переменной (аргумента) образуют область определения функции.
| D(f), D(y)
|
| 3.
| Область значения функции
| Все значения, которые принимает зависимая переменная у образуют область значений функции.
| E(f), Е (y)
|
| 4.
| График функции
| Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.
|
|
| 5.
| Возрастающая функция
| Функция называется возрастающей на множестве Х, если большему значению аргумента соответствует большее значение функции.
| если  , то , то 
|
| 6.
| Убывающая функция
| Функция называется убывающей на множестве Х, если большему значению аргумента соответствует меньшее значение функции.
| если  , то , то 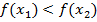
|
| 7.
| Монотонная функция
| Функция возрастающая на множестве Х или убывающая на множестве Х называется монотонной на множестве Х.
|
|
| 8.
| Чётная функция
| Функция  называется чётной, если область её определения симметрична относительно нуля и для любого значения аргумента называется чётной, если область её определения симметрична относительно нуля и для любого значения аргумента  верно равенство верно равенство

| График четной функции симметричен относительно оси ординат
|
| 9.
| Нечётная функция
| Функция  называется нечётной, если область её определения симметрична относительно нуля и для любого значения аргумента называется нечётной, если область её определения симметрична относительно нуля и для любого значения аргумента  верно равенство верно равенство

| График нечетной функции симметричен относительно начала координат
|
| 10.
| Нули функции
| Значения аргумента, при которых значения функции равны нулю.
| x при которых у=0
|
| 11.
| Промежутки знакопостоянства
| Промежутки, в которых функции с охраняет знак.
| Значения х, при которых 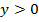 или или 
|
| 12.
| Ограниченная сверху
| Функция называется ограниченной сверху, если существует число b такое, что для любого аргумента х выполняется неравенство: f(x)  b. b.
|
|
| 13.
| Ограниченная снизу
| Функция называется ограниченной снизу, если существует числа а такое, что для любого аргумента х выполняется неравенство: a  f(x). f(x).
|
|
| 14.
| Ограниченная функция
| Функция называется ограниченной, если существует два числа а и b такие, что для любого аргумента х выполняется неравенство: a  f(x) f(x)  b. b.
|
|