Индуктивности коммутирующего контура
Задача расчета состоит в выборе конструкции катушки, определении ее геометрических размеров и обмоточных данных, которые должны обеспечить требуемые значения индуктивности. При этом температура обмоточного провода не должна превышать допустимого значения Наибольшее применение на практике получили катушки без ферромагнитного сердечника, имеющие цилиндрическую форму и квадратное сечение см. рис. 3.14. Для оптимальной конструкции средний диаметр катушки D связан с высотой сечения обмотки А соотношением D=3А [14]. При этом обеспечивается максимальная индуктивность
где
Рис. 3.14
Полагая, что в установившемся режиме процессы теплоотдачи определяются формулой Ньютона
где Р – мощность, выделяющаяся на активном сопротивлении обмотки R при протекании тока I (эффективное, действующее значение тока);
Для приведенной конструкции катушки
где
Преобразуя выражение 3.1–3.3, получим формулы для определения А и w
При выборе сечения провода следует учитывать, что ток в коммутирующей катушке имеет импульсный характер. Для переходных режимов работы ТКУ время выключения силового ключа
где Если ТКУ используется при редких отключениях, то коэффициент перегрузки по току для коммутирующей катушки рассчитывается по формуле [15]
где
|

 .
.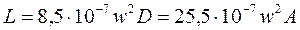 , (3.1)
, (3.1)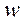 - число витков в обмотке.
- число витков в обмотке.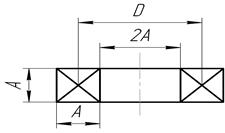
 , (3.2)
, (3.2) – коэффициент теплоотдачи с поверхности охлаждения катушки
– коэффициент теплоотдачи с поверхности охлаждения катушки 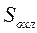 .
.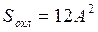 , тогда
, тогда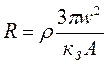 , (3.3)
, (3.3)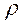 – удельное сопротивление материала провода обмотки при рабочей температуре;
– удельное сопротивление материала провода обмотки при рабочей температуре;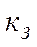 – коэффициент заполнения обмоточного окна.
– коэффициент заполнения обмоточного окна.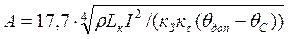 ; (3.4)
; (3.4)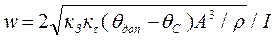 . (3.5)
. (3.5)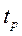 значительно меньше времени рабочего цикла
значительно меньше времени рабочего цикла 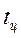 . При этом для большинства применений постоянная времени нагрева катушки
. При этом для большинства применений постоянная времени нагрева катушки 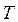 много больше, чем
много больше, чем  , следовательно, температура обмотки не достигает своего установившегося значения. В таких случаях при анализе теплового режима обмотки эффективное значение тока в катушке пересчитывают, используя коэффициент перегрузки по току
, следовательно, температура обмотки не достигает своего установившегося значения. В таких случаях при анализе теплового режима обмотки эффективное значение тока в катушке пересчитывают, используя коэффициент перегрузки по току 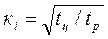 ,
,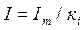 , (3.6)
, (3.6)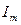 - амплитуда тока в
- амплитуда тока в 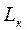 .
.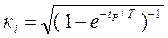 ,
,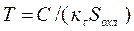 ;
; 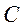 – общая теплоемкость провода катушки.
– общая теплоемкость провода катушки.


