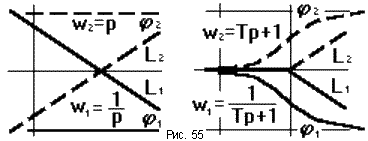
При построении ЧХ некоторых звеньев можно использовать “ правило зеркала ”: при k = 1 ЛАЧХ и ЛФЧХ звеньев с обратными передаточными функциями зеркальны относительно горизонтальной оси. Так на рис.55 изображены ЧХ идеального дифференцирующего и идеального орсирующего звеньев.
Если k  1, то передаточную функцию звена можно рассматривать как произведение W = k.W1, где W1 - передаточная функция с k = 1. При этом амплитуда вектора АФЧХ W(j
1, то передаточную функцию звена можно рассматривать как произведение W = k.W1, где W1 - передаточная функция с k = 1. При этом амплитуда вектора АФЧХ W(j  ) при всех значениях
) при всех значениях 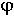 должна бытьувеличена в k раз, то есть A(
должна бытьувеличена в k раз, то есть A( ) = kA1(
) = kA1( ). Поэтому, например, центр полуокружности АФЧХ апериодического звена будет находиться не в точке P = 1/2, а в точке k/2. ЛАЧХ также изменится: L(
). Поэтому, например, центр полуокружности АФЧХ апериодического звена будет находиться не в точке P = 1/2, а в точке k/2. ЛАЧХ также изменится: L( ) = 20lgA(
) = 20lgA( ) = 20lgkA1(
) = 20lgkA1( ) = 20lgk + 20lgA1(
) = 20lgk + 20lgA1( ). Поэтому при k
). Поэтому при k  1 ЛАЧХ звена нужно поднять по оси ординат не меняя ее формы на 20lgk. На ЛФЧХ изменение k никак не отразится. Для примера на рис.56 приведены частотные характеристики апериодического звена при k = 10 и T = 1c. При этом ЛАЧХ апериодического звена с k = 1 поднята вверх на 20lg10 = 20.
1 ЛАЧХ звена нужно поднять по оси ординат не меняя ее формы на 20lgk. На ЛФЧХ изменение k никак не отразится. Для примера на рис.56 приведены частотные характеристики апериодического звена при k = 10 и T = 1c. При этом ЛАЧХ апериодического звена с k = 1 поднята вверх на 20lg10 = 20.

Вопросы
- Что называется частотными характеристиками?
- Как получить частотные характеристики опытным путем?
- Как получить частотные характеристики теоретическим путем по известной передаточной функции звена?
- Что такое и как получить АФЧХ?
- Что такое и как получить ВЧХ?
- Что такое и как получить МЧХ?
- Что такое и как получить АЧХ?
- Что такое и как получить ФЧХ?
- Что такое и как получить ЛАЧХ?
- Что такое и как получить ЛФЧХ?
- Как построить годограф АФЧХ?
- Постройте АФЧХ, ЛАЧХ и ЛФЧХ безынерционного звена.
- Постройте АФЧХ, ЛАЧХ и ЛФЧХ интегрирующего звена.
- Постройте АФЧХ, ЛАЧХ и ЛФЧХ апериодического звена.
- Постройте АФЧХ, ЛАЧХ и ЛФЧХ колебательного звена.
- Постройте АФЧХ, ЛАЧХ и ЛФЧХ консервативного звена.
- Постройте ЛАЧХ и ЛФЧХ идеального дифференцирующего звена.
- Постройте ЛАЧХ и ЛФЧХ идеального форсирующего звена.
- Как изменятся ЛАЧХ и ЛФЧХ звена, если коэффициент усиления возрастет в 100 раз?
- Для чего служит правило зеркала.


 1, то передаточную функцию звена можно рассматривать как произведение W = k.W1, где W1 - передаточная функция с k = 1. При этом амплитуда вектора АФЧХ W(j
1, то передаточную функцию звена можно рассматривать как произведение W = k.W1, где W1 - передаточная функция с k = 1. При этом амплитуда вектора АФЧХ W(j  ) при всех значениях
) при всех значениях 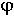 должна бытьувеличена в k раз, то есть A(
должна бытьувеличена в k раз, то есть A(



