Понятие частотных характеристик
Андриаманзака Ракатуманга Жан-Флорентин – философский жаб. Гиб – водяной конь. Лльяма (Волчонка) – отродье Темного Пламени Бездны. Серпьент Кулебрин – Хозяин Всея Крапивы и Сопредельного. Стражи Крови (Кошки Полнолуния) – обитатели дворца Анхеля.
[1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] Понятие частотных характеристик
Если подать на вход системы с передаточной функцией W(p) гармонический сигнал
то после завершения переходного процесса на выходе установится гармонические колебания
с той же частотой Подставим выражения для u(t) и y(t) в уравнение динамики (aоpn + a1pn - 1 + a2pn - 2 +... + an)y = (bоpm + b1pm-1 +... + bm)u. Учтем, что
а значит pnu = pnUmejwt = Um (jw)nejwt = (jw)nu. Аналогичные соотношения можно записать и для левой части уравнения. Получим:
По аналогии с передаточной функцией можно записать:
W(j W(j
Если W(j
В ТАУ широко используются логарифмические частотные характеристики (ЛЧХ) (рис.49): логарифмическая амплитудная ЧХ (ЛАЧХ) L(

lg(P2/P1) = lg(A22/A12) = 20lg(A2/A1). По оси абсцисс откладывается частота w в логарифмическом масштабе. То есть единичным промежуткам по оси абсцисс соответствует изменение w в 10 раз. Такой интервал называется декадой. Так как lg(0) = - ЛФЧХ, получаемая из второго слагаемого, отличается от ФЧХ только масштабом по оси ЧХ являются исчерпывающими характеристиками системы. Зная ЧХ системы можно восстановить ее передаточную функцию и определить параметры.
|



 , но иными амплитудой и фазой, зависящими от частоты
, но иными амплитудой и фазой, зависящими от частоты 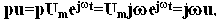
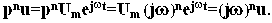
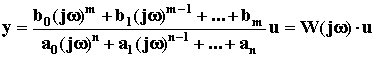 .
.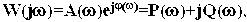 где P(
где P( (
(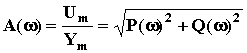 ;
; 
 его конец будет вычерчивать кривую, называемую годографом вектора W(j
его конец будет вычерчивать кривую, называемую годографом вектора W(j 






