Вопросы
1. Многомерное нормальное распределение и его свойства.
2. Выборочное среднее и выборочная ковариационная матрица. Распределение выборочного среднего в случае выборки из многомерного нормального распределения.
3. Критерий Хоттелинга.
4. Частный критерий Хоттелинга.
5. Критерий проверки гипотезы о равенстве средних двух нормальных генеральных совокупностей.
6. Понятие условного распределения. Условное распределение подмножества компонент нормально распределенного случайного вектора.
7. Понятие частного коэффициента корреляции.
8. Понятие множественного коэффициента корреляции и его свойства.
9. Корреляционный анализ порядковых признаков.
10. Корреляционный анализ качественных признаков.
11. Сущность задачи кластерного анализа. Различные виды расстояний между объектами и между кластерами в непараметрическом кластерном анализе.
12. Иерархический алгоритм кластерного анализа.
13. Метод k-средних в кластерном анализе.
Типовые задачи
- Случайный вектор
 имеет двумерное нормальное распределение
имеет двумерное нормальное распределение  . Найти 1) распределение
. Найти 1) распределение  , 2) распределение случайной величины
, 2) распределение случайной величины  , 3) распределение вектора
, 3) распределение вектора  .
. - Имеется выборка из 4 элементов из двумерного распределения:

.
Найти выборочное среднее, выборочную ковариационную матрицу и выборочный коэффициент корреляции.
- Пусть вектор
 имеет 3-х мерное нормальное распределение с ковариационной матрицей
имеет 3-х мерное нормальное распределение с ковариационной матрицей  . Вычислить все частные коэффициенты корреляции и множественный коэффициент корреляции
. Вычислить все частные коэффициенты корреляции и множественный коэффициент корреляции  .
. - Исследуется зависимость розничного товарооборота магазинов от числа работников. Имеются данные по этим экономическим показателям для 6 магазинов.
| Розничный товарооборот
|
|
|
|
|
|
|
| Число работников
|
|
|
|
|
|
|
С уровнем значимости 0.1 проверить гипотезу о независимости розничного товарооборота от числа работников при помощи а) обычного коэффициента корреляции б) рангового коэффициента корреляции.
- Из 200 абитуриентов, поступивших в институт, 43 имели золотые медали. По истечении года обучения 22 человека было отчислено. Среди отчисленных 4 медалиста. С уровнем значимости 0.1 проверить гипотезу о независимости признаков “отчислен – не отчислен” от наличия медали.
- Для анализа влияния витамина на профилактику простудных заболеваний 200 человек случайным образом были разделены на 2 равные группы. Одной группе дали витамин, другой – «пустышку», но всем пациентам было сказано, что им дали витамин. Результаты обследований приведены в таблице.
|
| Меньше простудных заболеваний
| Больше простудных заболеваний
| Без изменений
|
| Контрольная группа
|
|
|
|
| Группа, принимавшая витамин
|
|
|
|
С уровнем значимости 0,05 проверить гипотезу о независимости простудных заболеваний от приема витаминов.
- В кластер
 входят 4 объекта, расстояние от которых до объекта №5 составляет соответственно 2, 5, 6, 7. Чему равно расстояние от объекта №5 до кластера
входят 4 объекта, расстояние от которых до объекта №5 составляет соответственно 2, 5, 6, 7. Чему равно расстояние от объекта №5 до кластера  , если расстояние измеряется по принципу 1) ближайшего соседа 2)дальнего соседа 3) по принципу средней связи.
, если расстояние измеряется по принципу 1) ближайшего соседа 2)дальнего соседа 3) по принципу средней связи.
- Расстояние между пятью объектами характеризуется матрицей расстояний:
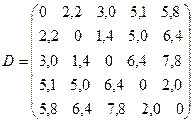
.
Чему равно расстояние между кластерами  и
и  , если расстояние измеряется по принципу 1) ближайшего соседа 2)дальнего соседа 3) по принципу средней связи.
, если расстояние измеряется по принципу 1) ближайшего соседа 2)дальнего соседа 3) по принципу средней связи.
 .
.
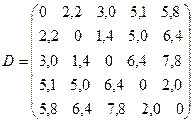 .
.

 имеет двумерное нормальное распределение
имеет двумерное нормальное распределение  . Найти 1) распределение
. Найти 1) распределение  , 2) распределение случайной величины
, 2) распределение случайной величины  , 3) распределение вектора
, 3) распределение вектора  .
. имеет 3-х мерное нормальное распределение с ковариационной матрицей
имеет 3-х мерное нормальное распределение с ковариационной матрицей  . Вычислить все частные коэффициенты корреляции и множественный коэффициент корреляции
. Вычислить все частные коэффициенты корреляции и множественный коэффициент корреляции  .
.  входят 4 объекта, расстояние от которых до объекта №5 составляет соответственно 2, 5, 6, 7. Чему равно расстояние от объекта №5 до кластера
входят 4 объекта, расстояние от которых до объекта №5 составляет соответственно 2, 5, 6, 7. Чему равно расстояние от объекта №5 до кластера  и
и  , если расстояние измеряется по принципу 1) ближайшего соседа 2)дальнего соседа 3) по принципу средней связи.
, если расстояние измеряется по принципу 1) ближайшего соседа 2)дальнего соседа 3) по принципу средней связи.


