Else begin

move(n - 1, s1, sk, sw);

step;

move(n-1, sw, s1, sk)

End

end;

Begin

read(m); {число дисков}

writeln('для ', m:3, ' дисков следует произвести ',

'следующие действия:');

move(m, left, middle, right);

readln

end.

 

 

Псевдослучайные числа. Функция, возвращающая значение и меняющая параметр

Программа на языке Паскаль:

Рассмотрим такую программу:

var s, i: integer;

function next(var seed: integer): integer;

Const

multiplier = 37;

increment = 3;

cycle = 64;

Begin

next:= seed;

seed:= (multiplier * seed + increment) mod cycle

end;

Begin

s:= 16;

writeln(next(s));

writeln(next(s));

writeln(next(s));

writeln(next(s));

s:= 16;

for i:= 1 to 64 do

write(next(s):3);

readln

end.

Примечания:

Использование var в заголовке – необычный прием для функции.

Будучи вызвана с параметром s, содержащим число 16, эта функция возвращает число 16. Вместе с тем, возвращая 16, функция изменяет значение, хранящееся в переменной seed (или s), на 19. Если функцию вызвать снова, с полученным значением s, то она возвратит число 19 и изменит значение s на 2. Продолжая вызывать функцию next, получим определенную последовательность целых чисел, начинающуюся с исходного значения s (цикл for).

Замечательным свойством этой последовательности является то, что каждое значение от 0 до 63 встречается в ней один раз. Более того, шестьдесят пятый вызов функции next дает число 16 и начинается новый цикл. Другими словами, начиная с любого желаемого целого, функция генерирует фиксированную перестановку чисел от 0 до 63.

Такой прием используется преимущественно для генерации "случайных" чисел (правильнее их называть псевдослучайными – чтобы подчеркнуть их предсказуемость). Цикл из 64 чисел, конечно, слишком мал; Грогоно предлагает константы для генерации перестановки чисел от 0 до 65 535:

const multiplier = 25173; increment = 13849; cycle = 65536;

Подбор констант с нужными свойствами – нетривиальная задача.

Приведенная выше функция возвращает значение и изменяет значение параметра. Такой способ действий применяется нечасто. В большинстве функций нет необходимости изменять параметры, и, следовательно, нет смысла использовать слово var в заголовке.

 

 

Процедура вычисления корней квадратного уравнения

Алгоритм решения задачи:

Представленная ниже программа с процедурой вычисления корней квадратного уравнения не возвращает в основную программу ничего (просто выводит результат на экран). Однако можно написать такую процедуру, которая будет использовать глобальные переменные x1 и x2. В результате в основной ветке программы можно будет использовать полученные корни квадратного уравнения.

Программа на языке Паскаль:

Var

a, b, c: real;

procedure sq (a,b,c: real);

var d, x1, x2: real;

Begin

d:= b * b - 4 * a * c;

if d >= 0 then begin

x1:= (-b + sqrt (d)) / (2 * a);

x2:= (-b - sqrt (d)) / (2 * a);

if x1 = x2 then

writeln ('x1 = ', x1:6:2)

Else

writeln ('x1 = ', x1:6:2, '; x2 = ', x2:6:2)

End

Else

writeln ('Корней нет!')

end;

Begin

write ('a = '); readln (a);

write ('b = '); readln (b);

write ('c = '); readln (c);

writeln (a:6:2,'x*x + ',b:6:2,'x + ',c:6:2,' = 0');

sq (a, b, c);

readln

end.

 

 

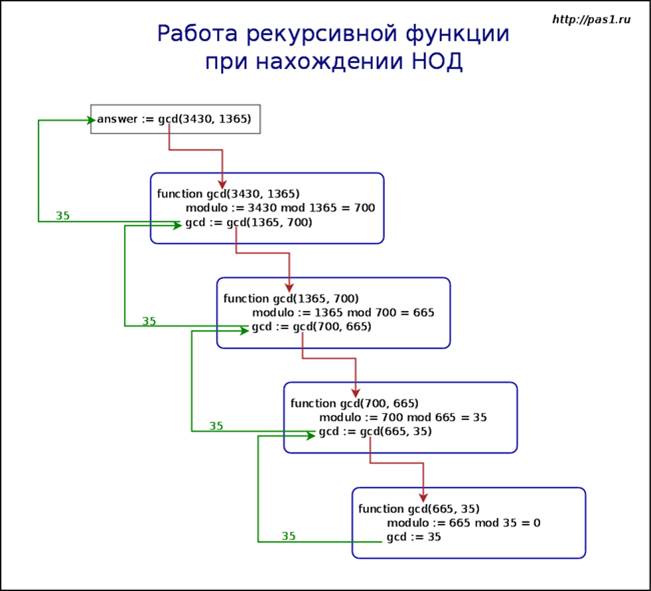
Нахождение НОД (наибольшего общего делителя) с помощью рекурсивной функции

Алгоритм решения задачи:

Наибольший общий делитель (НОД) чисел 3430 и 1365 – это 35. Другими словами, 35 – наибольшее число, на которое и 3430 и 1365 делятся без остатка. Чтобы убедиться в этом, разложим оба числа на простые сомножители:

3430 = 2 * 5 * 7 * 7 * 7

1365 = 3 * 5 * 7 * 13

и выделим пары общих сомножителей. В данном случае это пары 5 и 7. Наибольший общий делитель – это произведение совпадающих сомножителей; в данном случае это 5 * 7 = 35.

Более изящный метод поиска НОД – алгоритм Евклида. Найдем остаток от деления 3430 на 1365:

3430 mod 1365 = 700

Так как этот остаток не равен нулю, повторим то же действие, подставив вместо первого числа второе, а вместо второго – остаток:

1365 mod 700 = 665

Этот остаток также не нуль, поэтому еще одно деление:

700 mod 665 = 35

И еще одно:

665 mod 35 = 0

Теперь остаток – нуль, следовательно, НОД равен 35. Вот и отлично.

Следующая программа на Паскале использует метод Эвклида и рекурсию:

Программа на языке Паскаль:

var a, b, answer: integer;

function gcd(m, n: integer): integer;

var modulo: integer;

Begin

modulo:= m mod n;

if modulo = 0 then

gcd:= n

Else

gcd:= gcd (n, modulo)

end;

Begin

write('Enter two numbers: ');

readln(a, b);

answer:= gcd(a, b);

writeln('Greatest common divisor: ', answer);

readln

end.

Примечания:

Если представить, что в функцию сразу подставляются числа 665 и 35, то сразу ясно, как вычисляется gcd(665, 35): остаток modulo будет равен нулю и функция возвратит число 35 (ветка if). А вот при обращении gcd(3430, 1365) modulo будет равен 700, и, следовательно, функция вызовет себя еще раз в виде gcd(1365, 700). Таким образом, при каждом обращении Паскаль как бы создает новую копию функцииgcd:

 

 

Функция, вычисляющая наибольший общий делитель

Алгоритм решения задачи:

Оформление алгоритмов вычисления наибольшего общего делителя в виде функций удобно, если в задаче требуется несколько или множество раз использовать данный алгоритм, по отношению к различным исходным данным.

Программа на языке Паскаль:

Var

k, l, n: integer;

function nod (var a,b: integer): integer;

var c: integer;

Begin

Repeat