Прямоугольная диметрическая проекция
Прямоугольная диметрическая проекция Прямоугольная диметрическая проекция наряду с прямоугольной изометрической проекцией является наиболее распространённым видом аксонометрических проекций. Этот вид аксонометрической проекции обеспечивает наилучшую наглядность предмета, однако построение изображений в нем сложнее, чем в изометрии. Правила построения прямоугольной диметрической проекции установлены ГОСТ 2.317-69 «Аксонометрические проекции». Построение диметрической проекции предмета, как и любой другой аксонометрической проекции, выполняется по каркасу характерных для него точек с учётом свойств параллельного проецирования.
1.1. Положение осей и значения коэффициентов искажения
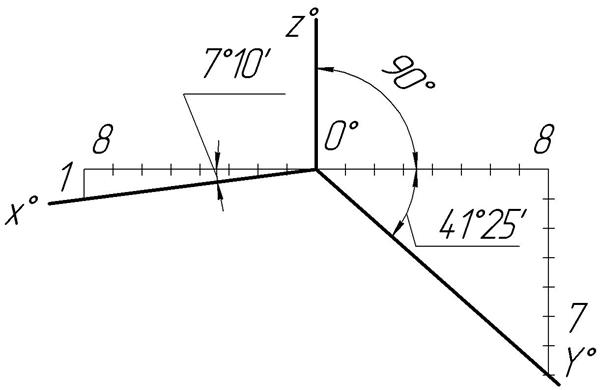
Положение осей в прямоугольной диметрии показано на рис.1. Практически оси X0 и Y0 удобно проводить как гипотенузы прямоугольных треугольников с отношением катетов 1:8 и 7:8.
Коэффициенты искажения по осям X0 и Z0 – 0,94, а по оси Y0 – 0,47. Однако при построении изображения в прямоугольной диметрии пользуются приведенными коэффициентами искажения, которые принимаются по осям X0 и Z0 равным 1, а по оси Y0 – 0,5. В результате этого изображение увеличивается в 1,06 раза. (1:0,94 Плоские фигуры в диметрической проекции строят уменьшая в двое все размеры по оси Y0.
1.2. Диметрическая проекция окружности
Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы (рис. 2).
В плоскости X0ОZ0 большая ось эллипса 1 (рис.2) равна Соотношение осей эллипсов 2 и 3, расположенных в плоскостях X0ОY0 и X0ОZ0, одинаково. Большая ось этих эллипсов равна Направление осей эллипсов 1,2 и 3 определяется по тому же правилу, что и для прямоугольной изометрии – большие оси эллипсов должны быть перпендикулярны свободным, т.е. отсутствующим в данных координатных плоскостях, аксонометрическим осям. Малые оси эллипсов при этом параллельны свободным осям (рис. 2). Например, в плоскости X0ОZ0 отсутствует ось Y0, значит большая ось эллипса 1 перпендикулярна оси Y0. Если плоскость изображаемой окружности занимает произвольное положение по отношению к координатным плоскостям, то эллипс, в который проецируется окружность, строится по точкам, как для произвольной кривой. Диметрические проекции окружностей, плоскости которых параллельны плоскостям проекций, рекомендуется строить одним из двух основных способов (в зависимости от размера окружности): а) по восьми характерным точкам с помощью лекала (рис. 3 и 4), когда диаметр изображаемой окружности небольшой – до 15 … 20 мм; б) как четырехцентровые овалы, очерченные дугами окружностей, – при больших размерах окружностей.
1.2.1. Построение эллипса по восьми точкам
На рис.3 изображён эллипс – диметрическая проекция окружности диаметра “ На рис. 4 изображён эллипс – диметрическая проекция окружности, лежащей в плоскости X0О Y0. Он также построен по восьми точкам – концами сопряжённых диаметров (точки
1.2.2. Построение овалов, заменяющих эллипсы
Построение овала, заменяющего диметрическую проекцию окружности, лежащей в плоскости X0ОY0 или Y0О Z0, показано на рис. 5.
Для построения овала: а) определяют положение осей овала; б) определяют размеры осей овала АВ = в) строят центры О1 , О2 , О3 и О4 сопряженных дуг окружностей, из которых состоит овал. Для этого откладывают размеры г) очерчивают овал четырьмя дугами (рис. 5, б). Радиусы этих дуг R1 и R2 получаются построением. Точки сопряжения дуг находятся на линиях, соединяющих центры дуг. Построение овала, заменяющего диметрическую проекцию окружности, лежащей в плоскости X0О Z0, показано на рис. 6.
Для построения овала: а) проводят аксонометрические оси Х0, Y0, Z0; б) определяют положение осей овала – большая ось перпендикулярна оси Y0, малая совпадает с осью Y0 (рис. 6.а). Определять размеры осей овала нет необходимости; в) на осях X0 и Z0 откладывают размеры сопряжённых диаметров овала, равные диаметру изображаемой окружности “ г) определяют положение центров О1, О2 , О3 и О4 сопряжённых дуг окружностей, которыми очерчен овал. Для этого из точек 10 и 20 проводят горизонтальные линии до пересечения с направлениями большой и малой осей овала; д) очерчивают овал четырьмя дугами радиусами R1 и R2 (рис. 6.б). Точками сопряжения дуг являются точки 10, 20, 30, 40.
1.3. Диметрическая проекция шара (сферы)
В прямоугольной диметрии сфера диаметром “
Для наглядности в аксонометрии часто изображают шар с вырезом одной восьмой части плоскостями, проходящими через центр шара и параллельными горизонтальной, фронтальной и профильной плоскостям проекций. Эти плоскости рассекают шар по главным окружностям – экватору и фронтальному и профильному меридианам. В диметрии главные окружности изображают в виде эллипсов, большие оси которых перпендикулярны свободным аксонометрическим осям. На рис. 7а и 7б показаны проекции шара и построение диметрии шара с вырезом одной четверти. Через центр шара – точку О0 проведены оси Х0, Y0 и Z0 прямоугольной диметрии. На осях Х0 и Z0 в обе стороны от точки О0 отложены отрезки, равные радиусу шара –
1.4. Диметрическая проекция линии пересечения поверхностей
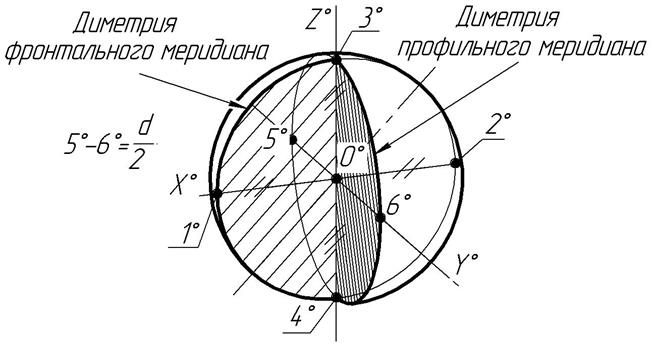
Аксонометрические проекции линии пересечения поверхностей строят по точкам. Эти точки находят или по их координатам, взятых с комплексного чертежа (рис. 8, 9), или способом вспомогательных секущих плоскостей непосредственно на аксонометрической проекции (рис. 10).
1.5. Выполнение разрезов и нанесение размеров
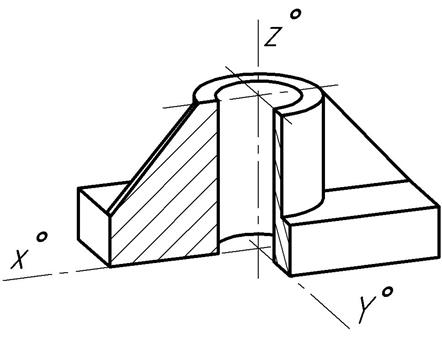
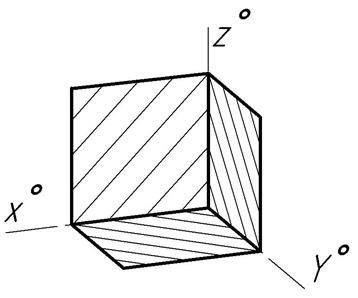
Если модель (деталь) имеет внутренние полости, отверстия, углубления, то для пояснения их формы и положения в аксонометрии выполняют разрезы (рис.11). Разрезы, как правило, выполняют плоскостями, параллельными координатным плоскостям. Секущие плоскости должны проходить через оси поверхностей вращения или совпадать с плоскостями симметрии предмета в целом или отдельных его элементов. При этом габариты модели (длина, ширина, высота) должны сохраниться. Места разреза должны быть полностью видимыми. Порядок построения разреза зависит от формы изображаемой детали. Существует два основных способа построения разрезов. По первому способу вначале строится аксонометрия детали без разреза, а затем вводятся секущие плоскости и выполняется разрез. Затем построения, относящиеся к той части предмета, которая должна быть исключена, убирают. Второй способ построения разреза заключается в том, что сначала строятся в аксонометрии сечения, а затем к ним пристраиваются остальные части изображаемого предмета (находящиеся позади секущих плоскостей). Этот способ сокращает количество построений по сравнению с предыдущим способом, но в то же время требует и более четкого представления формы изображаемой детали. Приведенные способы выполнения аксонометрического чертежа детали с разрезами не могут считаться единственно возможными. В практике выполнения аксонометрических разрезов предметов зачастую применяют комбинированный вариант, т.е. используют оба способа одновременно (одну часть предмета строят одним способом, а другую – другим). Штриховку сечений для различных секущих плоскостей выполняют в разные стороны (рис.11 и 12) в соответствии со следующим правилом: линии штриховки сечений должны быть параллельны одной из диагоналей изометрических проекций квадратов, лежащих в соответствующих координатных плоскостях. На рис.12 линии штриховки параллельны большим диагоналям проекций квадратов-ромбов.
1.6. Теневая штриховка аксонометрической проекции
Для придания аксонометрической проекции модели большей наглядности рекомендуется нанести на изображение теневую штриховку, показывающую распределение света на поверхностях предмета. Условно принимают, что источник света находится сверху, сзади и слева от рисующего, т. е. освещение левостороннее. Направление взгляда рисующего при этом перпендикулярно плоскости XZ. Направление штриховки зависит от формы предмета. Вертикальные плоскости штрихуются вертикальными прямыми. Принято считать, что горизонтальные плоскости наиболее освещенные. Поэтому их или совсем не штрихуют, или наносят редкие линии, параллельные аксонометрическим осям Х0 или Y0. Учитывая сравнительно небольшие размеры изделий машиностроения (например, по сравнению с объектами строительства), можно считать, что параллельные плоскости деталей одинаково освещены, поэтому частота теневых штрихов на таких плоскостях должна быть одинакова. Наклонные плоскости штрихуют прямыми, параллельными углу наклона плоскости. Цилиндрические и конические поверхности штрихуют прямыми, совпадающими с образующими этих поверхностей, боковые поверхности пирамиды – линиями, проходящими через ее вершину. На изображении сферических поверхностей и поверхностей вращения наносят криволинейные штрихи (части концентрических окружностей) разной толщины и с разными промежутками между штрихами. Освещенные поверхности штрихуют тонкими линиями на большом расстоянии друг от друга, а теневые более толстыми линиями, располагая их чаще.
|

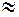 0,5:0,47
0,5:0,47 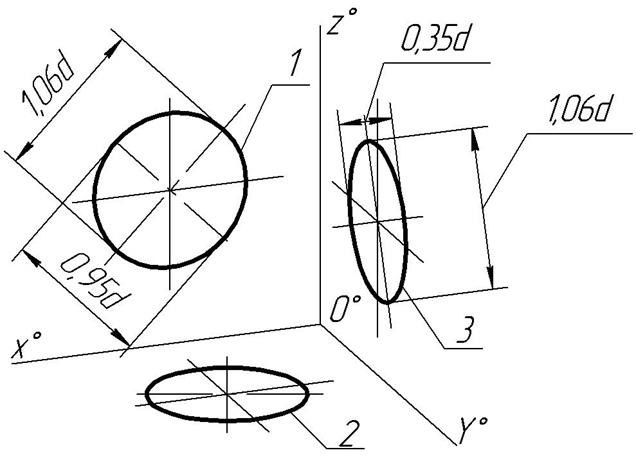
 , а малая –
, а малая – 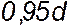 , где
, где 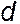 – диаметр изображаемой окружности.
– диаметр изображаемой окружности.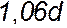 , а малая –
, а малая – 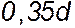 .
.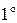 ,
, 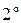 ,
,  ,
, 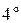 ) и концами большой и малой осей (точки А, В, С и D).
) и концами большой и малой осей (точки А, В, С и D).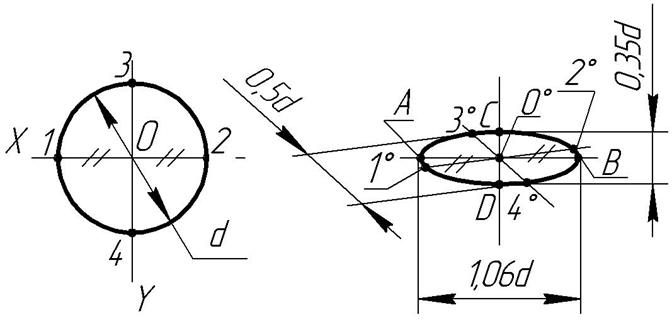

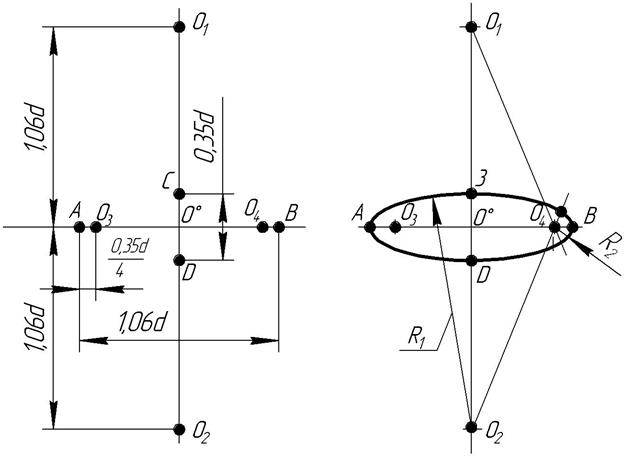
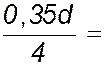
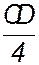 от точек А и В в направлении большей оси овала;
от точек А и В в направлении большей оси овала;
 , если приняты приведенные коэффициенты искажения – единица по осям Х0, Z0 и
, если приняты приведенные коэффициенты искажения – единица по осям Х0, Z0 и 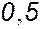 по оси Y0 (рис. 7).
по оси Y0 (рис. 7).
 , а на оси Y0 – отрезки, равные
, а на оси Y0 – отрезки, равные  , так как коэффициент искажения по оси Y0 равен
, так как коэффициент искажения по оси Y0 равен 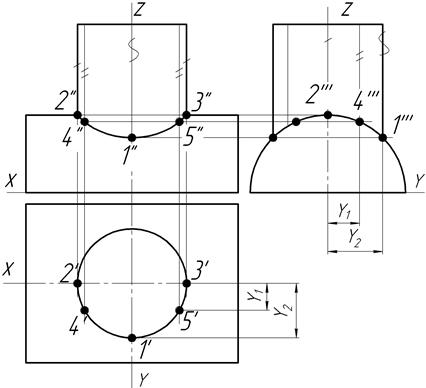 Рис.8. Комплексный чертеж модели
Рис.8. Комплексный чертеж модели
 Рис.9. Построение диметрической проекции линии пересечения поверхностей по координатам ее точек
Рис.9. Построение диметрической проекции линии пересечения поверхностей по координатам ее точек
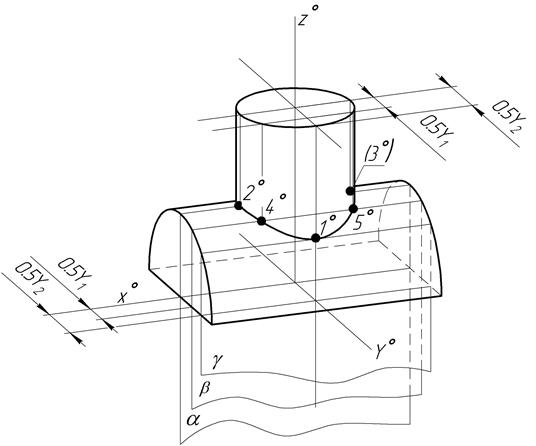 Рис.10. Построение диметрической проекции линии пересечения поверхностей способом вспомогательных секущих плоскостей
Рис.10. Построение диметрической проекции линии пересечения поверхностей способом вспомогательных секущих плоскостей