Низшие группы симметрии

1) Реутов О. А., Курц А. Л., Бутин К. П. - Органическая химия, т.1-4. -. - 2336с

2) Зоркий П. М. - Симметрия молекул и кристаллических структур. - 1986. - 232с

Алгоритм определения точечной группы симметрии

Допустим, что вы нашли все элементы симметрии в молекуле. К какой точечной группе симметрии отнести эти элементы?

Шаг 1.

Для начала надо определить, является ли группа симметрии высшей или низшей. Посчитайте количество поворотных осей, порядок которых больше 2. Если таковых осей как минимум две, то речь идёт о высшей группе симметрии. Если такая ось одна или таковые отсутствуют, то речь идёт о низшей.

Шаг 2.

Высшие группы симметрии

1) Самое главное, что в названии высшей группы симметрии имеется заглавная латинская буква (T, O или I). Определим её.

1.1) Если имеется элемент С₅, то это группа I.

1.2) Если имеется элемент С₄ (но нет С₅), то это группа O.

1.3) Если есть элемент С₃ (но нет элементов более высокого порядка), то это группа T.

1.4) Если каким-то чудом вы найдёте элемент симметрии С_n с n>5, то это будет группа K.

2) Наличие плоскостей симметрии приводит к добавлению к названию группы симметрии индексов.

2.1) Если имеются плоскости симметрии, лежащие в координатных плоскостях, то добавляется индекс h.

2.1.1) Группу I_h имеет икосаэдр.

2.1.2) Группу O_h имеет октаэдр. Поскольку эту фигуру представить легко, можно убедиться, что она имеет группу симметрии O_h.

2.2) Группа T может иметь индекс d. Он появляется при наличии диагональных плоскостей симметрии, которые не лежат в координатных плоскостях. Группу T_d имеет тетраэдр, или молекула метана.

Низшие группы симметрии

1) С₁ не содержит ничего, кроме поворотной оси С₁. Такую группу имеет молекула, изображённая на картинке.

2) C_s содержит исключительно плоскость симметрии (в довесок – элемент S₁).

3) Группа C_i содержит исключительно центр инверсии (в довесок – элемент S₂).

4) Группа C_n (где n – целое число) содержит исключительно поворотную ось C_n. Группу С _∞ имеет вращающийся конус.

5) Группа S_n (где n >2) содержит исключительно элемент S_n (в довесок – элемент C_n/2). Группу S₄ содержит молекула, изображённая на рисунке в двух проекциях. Нарисовано не совсем удачно.

6) Группа С_nv включает в себя поворотную ось n-го порядка и n плоскостей симметрии, в которых лежит эта поворотная ось. Группу С _{∞ v} содержит конус.

7) Группа С_nh включает в себя поворотную ось n-го порядка и перпендикулярную ей плоскость симметрии. Группу С _{∞ h} содержит вращающийся цилиндр.

 

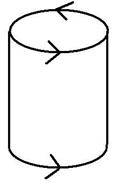
8) Группа D_n имеет элементы C_n и C₂┴C_n. Группу D _∞ содержит крученый цилиндр.

9) Группа D_nh имеет элементы C_n, C₂┴C_n и плоскость симметрии, перпендикулярную главной оси. Группу D _{∞ h} имеет цилиндр.

10) Группа D_nd имеет элементы C_n, C₂┴C_n и плоскости симметрии, диагональные по отношению к поворотным осям.

Литература

1) Реутов О. А., Курц А. Л., Бутин К. П. - Органическая химия, т.1-4. -. - 2336с

2) Зоркий П. М. - Симметрия молекул и кристаллических структур. - 1986. - 232с