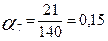Типовая задача. Пять экспертов о семи объектах экспертизы Q составили следующие ранжированные ряды по возрастающей шкале порядка:
* модели искусственных систем (инженерные сооружения);
* модели абстрактных систем (кибернетические);
* системы человеческой деятельности (СЧД), ориентированные на системные представления целенаправленных действий, тесно связанных с участием в них людей (системы управления, в частности государственного).
Для одной проблемной ситуации имеется, как правило, не одна модель, а «пучок», или даже «пучки» СЧД, воплощаю
Пять экспертов о семи объектах экспертизы Q составили следующие ранжированные ряды по возрастающей шкале порядка: эксперт №1 – Q5 Q3 Q2 Q1 Q6 Q4 Q7 эксперт №2 – Q5 Q3 Q2 Q6 Q4 Q1 Q7 эксперт №3 - Q3 Q2 Q5 Q1 Q6 Q4 Q7 эксперт №4 - Q5 Q3 Q2 Q1 Q4 Q6 Q7 эксперт №5 - Q5 Q3 Q1 Q2 Q6 Q4 Q7 Место объекта в ранжированном ряду называется его рангом. Численное значение ранга в ряду возрастающей шкалы порядка увеличивается от 1 до m (m – количество оцениваемых объектов). В данном примере m =7. 4. Определение суммы рангов каждого из объектов экспертной оценки. В рассматриваемом примере они: Q – 4+6+4+4+3=21; Q – 3+3+2+3+4=15; Q – 2+2+1+2+2=9; Q – 6+5+6+5+6=28; Q – 1+1+3+1+1=7; Q – 5+4+5+6+5=25; Q – 7+7+7+7+7=35. 5. На основании полученных сумм рангов строятся обобщенный ранжированный ряд. Для нашего примера он: Q5 Q3 Q2 Q1 Q6 Q4 Q7 6. Обобщенные экспертные оценки качества рассматриваемых объектов экспертизы, то есть коэффициенты их весомости, рассчитываются по формуле:
где n – количество экспертов; m – число оцениваемых показателей; Qij – коэффициент весомости j -го показателя в рангах (баллах), которой дал i –й эксперт. Расчеты по этой формуле для рассматриваемого примера дают следующие результаты:
Анализируя данные, полученные экспертным методом оценки качества, можно не только узнать, какой объект лучше или хуже других, но и на сколько. ЗАДАНИЕ №3 Определение экономического эффекта
|

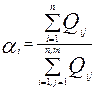 , (1)
, (1) ;
; 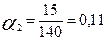 ;
;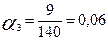 ;
;  ;
;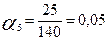 ;
;  ;
;