Математична модель
1. Скласти рівняння кола, яке проходить через точки (3;0) і (-1;2), якщо його центр лежить на прямій х-у+2=0. 2. Скласти канонічне рівняння еліпса, якщо еліпс проходить через точки М1(1;3) і М2(4;1). 3. Скласти рівняння гіперболи, фокуси якої розташовані на осі абсцис симетрично відносно початку координат, знаючи, крім того, що відстань між фокусами 2с=6 і ексцентриситет дорівнює 3/2. 4. Скласти рівняння параболи, яка має фокус (0;-3) і проходить через початок координат, знаючи, що її віссю є Оу. 5. Скласти канонічне рівняння параболи, якщо директриса має рівняння у+12=0. 6. Дано рівняння гіперболи Самостійна робота №3 Тема роботи: Технологія оптимізації, оптимальний бізнес-план, план по продукції. Мета роботи:Навчитися складати оптимальний план виробництва продукції з врахуванням обмеженого забезпечення матеріальними ресурсами. Засвоїти методику і технологію оптимізації планів в ТП Excel за допомогою програми Поиск решения. ТЕОРЕТИЧНІ ВІДОМОСТІ Визначення проблеми:На виробничому підприємстві „Електроприлад” склад готової продукції пустує. В цей же час цехи заповнені незавершеною продукцією. Немає реалізації, прибутку, зарплати, розвитку. Був складений план виробництва, в якому не були враховані обсяги запасів матеріалів і комплектуючих на складах і обмежені можливості постачальників вузлів і деталей. Проблема: менеджери і економісти розробили план виробництва продукції без врахування ресурсів, інакше запасів матеріалів і комплектуючих на складах і можливостей постачальників. Мета виробництва – максимально можливий прибуток. Потрібно визначити: планову кількість продукції і прибуток. Коефіцієнт зменшення віддачі відображає ефективність росту продажу за рахунок росту затрат на рекламу та інші витрати в системі маркетингу і збуту. Математична модель Уведемо позначення: i - номер рядка, ресурсу; j - номер стовпчика, продукту; Xj – планова кількість j-го продукту; Рj – прибуток на одиницю j-го продукту; Ві – обмежений запас і-го ресурсу на складі; Rij – норма витрату і-го ресурсу на одиницю j-го продукту; Сі – планова сума витрату і-го ресурсу по всім продуктам. В загальному вигляді дана модель економіко-математичної постановки задачі буде мати наступний вигляд: Ci= Цільова функція (максимізувати прибуток)
при обмеженнях Ci <= Ві та невід’ємній кількості продуктів Xj>=0.
|

 . Скласти його полярне рівняння її лівої вітки, вважаючи, що напрям полярної осі співпадає з доданім напрямом осі абсцис, а полюс знаходиться в лівому фокусі гіперболи.
. Скласти його полярне рівняння її лівої вітки, вважаючи, що напрям полярної осі співпадає з доданім напрямом осі абсцис, а полюс знаходиться в лівому фокусі гіперболи.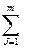 Rij*Xj,
Rij*Xj, Р=
Р= 


