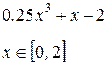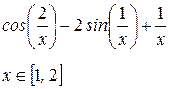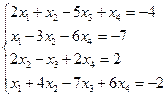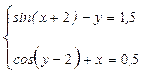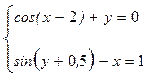Студопедия Главная Случайная страница Обратная связь

Разделы: Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Лабораторна робота № 4. Завдання № 1 Побудувати графік функції f (x) і приблизно визначити один з коренів рівняння


Завдання № 1 Побудувати графік функції f (x) і приблизно визначити один з коренів рівняння. Вирішити рівняння f (x) = 0 за допомогою вбудованої функції MathCAD root.

Варіант f (x) Варіант f (x)
   
   
   
   
   
   
   
   

 

Завдання № 2

Для полінома g (x) виконати наступні дії:

1. за допомогою команди Символи ® Коефіцієнти полінома створити вектор V, що містить коефіцієнти полінома;

2. вирішити рівняння g (x) = 0 за допомогою функції polyroots;

3. вирішити рівняння символьно, використовуючи команду Символи ® Змінні ® Обчислити.

Варіант g (x) Варіант g (x)
  x 4 - 2 x3 + x 2 - 12 x + 20   x 4 + x3 - 17 x 2 - 45 x - 100
  x 4 + 6 x3 + x 2 - 4 x - 60   x 4 - 5 x3 + x 2 - 15 x + 50
  x 4 - 14 x 2 - 40 x - 75   x 4 - 4 x3 - 2 x 2 - 20 x + 25
  x 4 - x3 + x 2 - 11 x + 10   x 4 + 5 x3 + 7 x 2 + 7 x - 20
  x 4 - x3 - 29 x 2 - 71 x -140   x 4 - 7 x3 + 7 x 2 - 5 x + 100
  x 4 + 7 x3 + 9 x 2 + 13 x - 30   x 4 + 10 x3 +36 x 2 +70 x + 75
  x 4 + 3 x3 - 23 x 2 - 55 x - 150   x 4 + 9 x3 + 31 x 2 + 59 x + 60
  x 4 - 6 x3 + 4 x 2 + 10 x + 75   15x4-6 x3+4x2 -12 x-10

 

 

Завдання № 3

Вирішити систему лінійних рівнянь:

1. матричним способом і використовуючи функцію lsolve;

2. методом Гауса;

3. використовуючи функцію Find.

Варіант Система лінійних рівнянь Варіант Система лінійних рівнянь
   
   
   
   
   
   
   
   

 

Завдання № 4

Перетворити нелінійні рівняння системи до виду f 1 (x) = y і f 2 (y) = x.

Побудувати їх графіки і визначити початкове наближення рішення.

Вирішити систему нелінійних рівнянь за допомогою функції Minerr.

Варіант Система нелінійних рівнянь Варіант Система нелінійних рівнянь
   
   
   
   
   
   
   
   

 

Завдання № 5 Символьно вирішити системи рівнянь.

 

Контрольні питання

1. Як можна вирішити нелінійне рівняння в MathCAD?

2. Як знайти початкове наближення кореня рівняння?

3. Для чого використовується функція polyroots?

4. Як можна вирішити систему лінійних рівнянь?

5. Як можна вирішити систему нелінійних рівнянь?

Лабораторна робота № 4

Тема: “РОЗРОБКА ПЛАНУ ПРИМІЩЕНЬ КОМЕРЦІЙНОГО БАНКУ І ПЛАНУ КОМП’ЮТЕРНОЇ МЕРЕЖІ”

Мета роботи: отримати навички проектування плану приміщень комерційних банків і плану комп’ютерної мережі з використанням інструментального засобу Microsoft Office Visio 2007.

 

Методичні вказівки:



<== предыдущая лекция | следующая лекция ==>
Формування статутного капіталу | 

Дата добавления: 2015-09-19; просмотров: 471. Нарушение авторских прав; Мы поможем в написании вашей работы!


Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений...


Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...


Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...


Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...

Растягивание костей и хрящей. Данные способы применимы в случае закрытых зон роста. Врачи-хирурги выяснили...

ФАКТОРЫ, ВЛИЯЮЩИЕ НА ИЗНОС ДЕТАЛЕЙ, И МЕТОДЫ СНИЖЕНИИ СКОРОСТИ ИЗНАШИВАНИЯ Кроме названных причин разрушений и износов, знание которых можно использовать в системе технического обслуживания и ремонта машин для повышения их долговечности, немаловажное значение имеют знания о причинах разрушения деталей в результате старения...

Различие эмпиризма и рационализма Родоначальником эмпиризма стал английский философ Ф. Бэкон. Основной тезис эмпиризма гласит: в разуме нет ничего такого...

Седалищно-прямокишечная ямка Седалищно-прямокишечная (анальная) ямка, fossa ischiorectalis (ischioanalis) – это парное углубление в области промежности, находящееся по бокам от конечного отдела прямой кишки и седалищных бугров, заполненное жировой клетчаткой, сосудами, нервами и...

Основные структурные физиотерапевтические подразделения Физиотерапевтическое подразделение является одним из структурных подразделений лечебно-профилактического учреждения, которое предназначено для оказания физиотерапевтической помощи...

Почему важны муниципальные выборы? Туристическая фирма оставляет за собой право, в случае причин непреодолимого характера, вносить некоторые изменения в программу тура без уменьшения общего объема и качества услуг, в том числе предоставлять замену отеля на равнозначный...

Studopedia.info - Студопедия - 2014-2025 год . (0.014 сек.) русская версия | украинская версия