Пусть передаточную функцию разомкнутой системы можно представить в виде
 ,
,
где передаточная функция  обладает свойством
обладает свойством  . Тогда передаточная функция замкнутой системы по ошибке равна
. Тогда передаточная функция замкнутой системы по ошибке равна
 .
.
Установившееся значение ошибки при постоянном входном сигнале  , имеющем изображение по Лапласу
, имеющем изображение по Лапласу  , может быть вычислено по теореме о конечном значении:
, может быть вычислено по теореме о конечном значении:
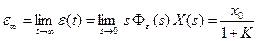 .
.
Таким образом, при увеличении коэффициента усиления  ошибка уменьшается (однако запас устойчивости также уменьшается и система может стать неустойчивой). Величина
ошибка уменьшается (однако запас устойчивости также уменьшается и система может стать неустойчивой). Величина  называется добротностью системы. При любом конечном
называется добротностью системы. При любом конечном  в такой системе ошибка будет конечной. Для линейно возрастающего сигнала ошибка будет линейно возрастать.
в такой системе ошибка будет конечной. Для линейно возрастающего сигнала ошибка будет линейно возрастать.
Теперь пусть 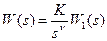 ,
,
где  – целое число и
– целое число и  .. Тогда для всех входных сигналов вида
.. Тогда для всех входных сигналов вида

система будет обеспечивать нулевую установившуюся ошибку при любых значениях коэффициентов  . Таким образом, при
. Таким образом, при  система отслеживает постоянный сигнал без установившейся ошибки. Такие системы называют астатическими.
система отслеживает постоянный сигнал без установившейся ошибки. Такие системы называют астатическими.
Число  называется порядком астатизма. Для сигнала
называется порядком астатизма. Для сигнала 
установившаяся ошибка равна 
Выше рассмотрен случай астатизма по отношению к задающему воздействию. Аналогично может идти речь об астатизме по отношении к возмущающему воздействию.

 ,
, обладает свойством
обладает свойством  . Тогда передаточная функция замкнутой системы по ошибке равна
. Тогда передаточная функция замкнутой системы по ошибке равна .
. , имеющем изображение по Лапласу
, имеющем изображение по Лапласу  , может быть вычислено по теореме о конечном значении:
, может быть вычислено по теореме о конечном значении: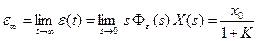 .
. ошибка уменьшается (однако запас устойчивости также уменьшается и система может стать неустойчивой). Величина
ошибка уменьшается (однако запас устойчивости также уменьшается и система может стать неустойчивой). Величина 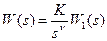 ,
, – целое число и
– целое число и 
 . Таким образом, при
. Таким образом, при  система отслеживает постоянный сигнал без установившейся ошибки. Такие системы называют астатическими.
система отслеживает постоянный сигнал без установившейся ошибки. Такие системы называют астатическими.




