Первая модификация метода Ньютона выполняется по формуле
xi+1 = xi – y(xi)/y`(x0), т.е. на каждой итерации используется константное значение производной y`(x0) Вторая итерация в предыдущем разделе выполняется по формуле x2 = x1 – y(x1)/y`(x0) = 2.8333-(2.8333^2-8)/(2*3) = 2.8287. 5. Для заданного интеграла найдите оценку по формуле трапеций при фиксированном числе разбиений интервала (N=4). S= 5.1 Формула трапеций для интеграла S= S=h/2 *[f(x0)+2*f(x1)+2*f(x2)+2*f(x3)+f(x4)], где h=(b-a)/N; x0=a; x1=a+h; x2=x1+h; x3=x2+h; x4=x3+h=b. 1. a=0; b=1; h=(1-0)/4=0.25; составим таблицу
S=0.25/2*[0-2* 0.1875-2*0.25-2*0.1875+0]= -0.1563
5.2 Формула Симпсона для интеграла S= S=h/3 *[f(x0)+4*f(x1)+2*f(x2)+4*f(x3)+f(x4)] и расчет предыдущего интеграла дает: S=0.25/3*[0-4* 0.1875-2*0.25-4*0.1875+0]= -0.1667
6. Для заданной функции постройте ее график в разумном диапазоне для поиска точек ее локальных экстремумов (наибольшего и наименьшего значений). Н айдите наибольшее значение взятием производной и решением возникающего уравнения f'(x)=0. f(x)=2x3-8x2-65x+10 Вычислим несколько значений функции: f(-3)=79; f(-2)=92; f(-1)=65; f(0)=10; f(1)=-61; экстремум типа максимума ожидается в районе x=-2. Н айдем наибольшее значение взятием производной и решением возникающего уравнения f'(x)=0. Запишем производную f’(x)=6x^2-16*x-65 и решим квадратное уравнение 6x^2-16*x-65 = 0; корни x1=-2,218; x2=4,885. Экстремум типа локального максимума находится в точке x=-2,218.
7. Рассчитать коэффициенты полинома второй степени по интерполяционной формуле Ньютона, используя таблицу значений исходной функции Задана таблица значений исходной функции
Где i=0,1,2. Рассчитаем таблицу разделенных разностей:
Интерполяционная формула Ньютона: P2(x)=y0+(x-x0)*y(x0,x1)+(x-x0)*(x-x1)*y(x0,x1,x2)=4+(x-0)*1+(x-0)*(x-1)*4= =4+x+4*x^2-4*x=4*x^2-3*x+4; коэффициенты полинома P=[4 -3 4]. 8. Текст завдання Рассчитать коэффициент полинома первой степени при x (при x в нулевой степени) по методу наименьших квадратов, используя таблицу «зашумленных» значений исходной функции. Таблица «зашумленных» значений исходной функции x= -3 -1 1 3 5 y= -1.49 -3.44 -6.49 -7.51 -11.07 Рассчитать коэффициенты полинома первой степени Составим таблицу:
В предпоследней строке вычислены суммы по столбцам; это коэффициенты системы двух линейных алгебраических уравнений AX=B A= x1=(-30+5*1.16)/5=-4.84; таким образом, решение этой системы (-4.84; -1.16) определяет коэффициенты аппроксимирующего полинома первой степени. 9. Рассчитать приближенные значения первой производной по таблице значений функции y=sin(x), используя симметричную и несимметричную схемы в точке x= 2; Сравнить с точным значением производной. x= -3 -2 -1 0 1 2 3 4 5 y= -0.1411 -0.9093 -0.8415 0 0.8415 0.9093 0.1411 -0.7568 -0.9589 Симметричная схема расчета первой производной в точке x=2: dy/dx ≈ [y(3)-y(1)]/(3-1) = (0.1411-0.8415)/2= -0.3502.
Несимметричная схема расчета первой производной в точке x=2: dy/dx ≈ [y(2)-y(1)]/(2-1)= (0.9093-0.8415)/1 = 0.0678. Точное значение по формуле первой производной dy/dx=cos(2)= -0.4161. Симметричная схема дает лучше результат по сравнению с несимметричной.
|


 при числе разбиений интервала интегрирования на N=4 частей имеет вид:
при числе разбиений интервала интегрирования на N=4 частей имеет вид: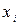
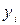
 B=
B=  , или
, или  ; вычитаем из 1-ого 2-ое уравнение и получаем x2=(-30+76.46)/(-40)=-1.16; Подставляем в первое уравнение и получаем
; вычитаем из 1-ого 2-ое уравнение и получаем x2=(-30+76.46)/(-40)=-1.16; Подставляем в первое уравнение и получаем


