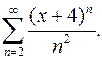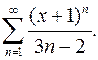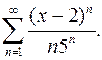Задания для контрольных работ
Задача 2. Решить систему линейных уравнений: а) по формулам Крамера; б) методом Гаусса; в) матричным методом. Сделать проверку.
Задача 3. Даны координаты вершин пирамиды Требуется: 1) записать векторы 2) найти модуль и направляющие косинусы вектора 3) вычислить скалярное произведение векторов 4) найти
Задача 4. Построить треугольник, вершины которого находятся в точках 1) уравнение сторон 2) уравнение высоты, проведенной из вершины 3) уравнение прямой, проходящей через вершину Задача 6. Решить уравнение
Задача 7. Найти пределы 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Задача 8. Найти производные
Задача 9. Найти интервалы монотонности и точки экстремума, установить интервалы выпуклости и точки перегиба графика функции
Задача 10. Найти частные производные второго порядка
Задача 14. Найти неопределенные интегралы.
Задача 15. Вычислить определенные интегралы.
Задача 17. Вычислить площадь фигуры, ограниченной параболой и прямой. Сделать чертеж. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Задача. 18. С помощью двойного интеграла вычислить площадь указанной области 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Задача 19. Изменить порядок интегрирования.
Задача 21. Исследовать сходимость числового ряда.
Задача 22. Найти интервал сходимости степенного ряда.
|



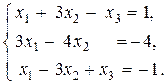
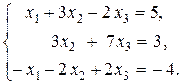

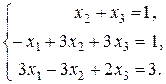
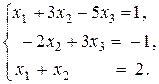
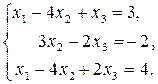

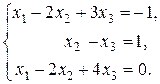
 .
. ,
, 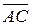 ,
,  в ортонормированном базисе
в ортонормированном базисе 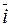 ,
,  ,
,  ;
; и
и  ;
;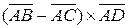 .
. ,
,  и
и 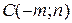 и найти:
и найти: и
и  ;
;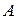 ;
; . Найденные решения изобразить точками на комплексной плоскости и найти модуль и аргумент одного из решений.
. Найденные решения изобразить точками на комплексной плоскости и найти модуль и аргумент одного из решений.



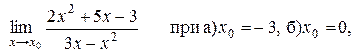
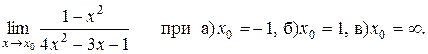

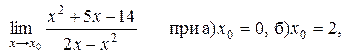
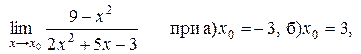

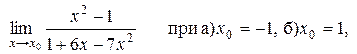
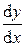 заданных функций.
заданных функций.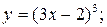
 ;
;
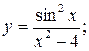

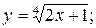




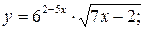


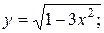
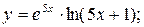




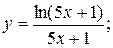
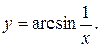
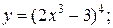

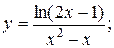





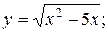



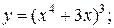
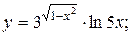




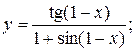
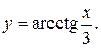
 .
.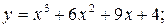

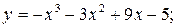
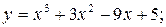



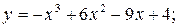
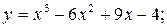
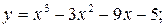
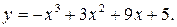



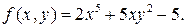
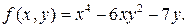

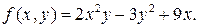



 ;
;
 ;
;
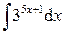 ;
;
 ;
;
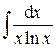 .
.
 .
.
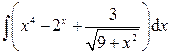 ;
;
 ;
;
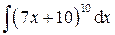 ;
;
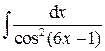 ;
;
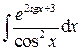 .
.
 .
.
 ;
;
 ;
;
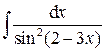 ;
;
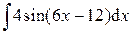 ;
;
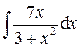 .
.
 .
.
 ;
;
 ;
;
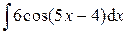 ;
;
 ;
;
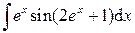 .
.
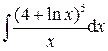 .
.
 ;
;
 ;
;
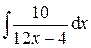 ;
;
 ;
;
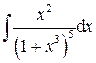 .
.
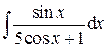 .
.
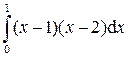 ;
;
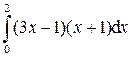 ;
;
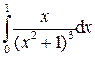 .
.
 .
.
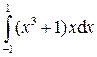 ;
;
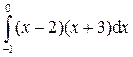 ;
;
 .
.
 .
.
 ;
;
 ;
;
 .
.
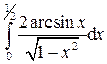 .
.
 ;
;
 ;
;
 .
.
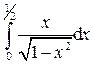 .
.
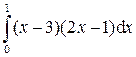 ;
;
 ;
;
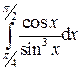 .
.
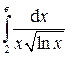 .
.
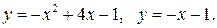
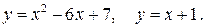



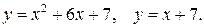


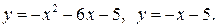
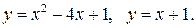
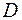 .
.
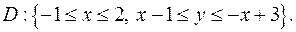
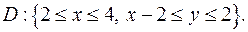

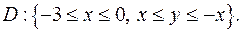
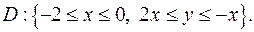

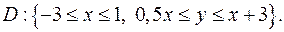
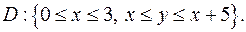
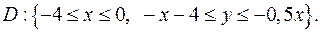
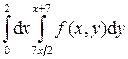 .
.
 .
.
 .
.
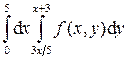 .
.
 .
.
 .
.
 .
.
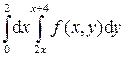 .
.
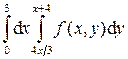 .
.
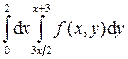 .
.
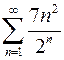 .
.
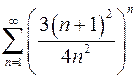 .
.
 .
.
 .
.
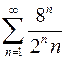 .
.
 .
.
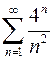 .
.
 .
.
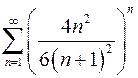 .
.
 .
.