Задания на контрольную работу
по разделу «Математика»
Вариант 1 1. Даны два множества: А = {6 k + 1½ k = 0, 1, 2,…} и B = {3 m + 4½ m = 0, 1, 2,…}. Найти: а) А È В; б) А Ç В; в) В \ А;г) А \ В; д) А ∆ В. 2. Даны два множества: А = {1, 3} и B = {2, 4, 5, 6}. Найти декартово произведение: а) А ´ В; б) В ´ А. 3. Даны три множества: А - множество натуральных чисел, делящихся нацело на 6; B - множество натуральных чисел, делящихся нацело на 10; С - множество натуральных чисел, делящихся нацело на 21. Определить, принадлежит ли число s = 96 множеству D = (А \ В) È (А Ç C) È (B Ç C)? Показать это число на диаграмме Венна, иллюстрирующей множество D. 4. Среди 24 студентов одним английским языком владеют 15 человек, немецким и английским - 2 человека. Не владеет (например, изучал французский или испанский) ни английским, ни немецким - 1 человек. Сколько студентов владеет только немецким языком? 5. Если N – множество натуральных чисел, М - множество положительных чисел, Р - множество простых чисел, Q - множество положительных нечётных чисел. Указать истинность высказываний: а) 6. Даны два множества: А = {6 k + 1½ k = 0, 1, 2,…} и B = {3 m + 4½ m = 0, 1, 2,…}. Установите, является ли соответствие f: A ® B, заданное формулой 7. Найти область определения функции 8. Найти предел функции 9. Правильно ли рассуждение, имеющее форму: «Все х являются у и ни одно х не является z; значит, все у не являются z»? 10. Построить таблицу истинности для высказывания
11. Доказать методом математической индукции, что при любом натуральном п справедливо следующее равенство:
12. Найти обратную подстановку произведения (АВС)-1 при А = 13. Найдите производную функции 14. Вычислите интеграл 15. Переведите с точностью до 5 знаков после запятой число 21,48(10) в двоичную, восьмеричную и шестнадцатеричную систему.
Вариант 2 1. Даны два множества: А = {2 k + 1½ k = 0, 1, 2,…} и B = {3 m ½ m = 0, 1, 2,…}. Найти: а) А È В; б) А Ç В; в) В \ А;г) А \ В; д) А ∆ В. 2. Даны два множества: А = {2, 3} и B = {1, 2, 3, 4}. Найти декартово произведение: а) А ´ В; б) В ´ А. 3. Даны три множества: А - множество натуральных чисел, делящихся нацело на 6; B - множество натуральных чисел, делящихся нацело на 10; С - множество натуральных чисел, делящихся нацело на 21. Определить, принадлежит ли число s = 105 множеству D = (А \ В) È (А Ç C) È (B Ç C)? Показать это число на диаграмме Венна, иллюстрирующей множество D. 4. В группе 30 студентов. Все, кроме двух, по итогам экзаменационной сессии имеют оценки «удовлетворительно» («3»), «хорошо» («4») и «отлично» («5»). Число студентов, имеющих оценки «5» - двенадцать, «4» - четырнадцать, «3» - шестнадцать. Трое учатся лишь на «5» и «3», трое – лишь на «5» и «4» и четверо – лишь на «4» и на «3». Сколько студентов сдали экзаменационную сессию только на «5»? 5. Если N – множество натуральных чисел, М - множество положительных чисел, Р - множество простых чисел, Q - множество положительных нечётных чисел. Указать истинность высказываний: а) 6. Даны два множества: А = {2 k + 1½ k = 0, 1, 2,…} и B = {3 m ½ m = 0, 1, 2,…}. Установите, является ли соответствие f: A ® B, заданное формулой 7. Найти область определения функции 8. Найти предел функции 9. Правильно ли рассуждение, имеющее форму: «Все х не являются у и некоторые х являются z; значит, все у не являются z»? 10. Построить таблицу истинности для высказывания
11. Доказать методом математической индукции, что при любом натуральном п справедливо следующее равенство:
12. Найти обратную подстановку произведения (АВС)-1 при А = 13. Найдите производную функции 14. Вычислите интеграл 15. Переведите с точностью до 5 знаков после запятой число 17,24(10) в двоичную, восьмеричную и шестнадцатеричную систему.
Вариант 3 1. Даны два множества: А = {3 k + 3½ k = 0, 1, 2,…} и B = { m + 2½ m = 0, 1, 2,…}. Найти: а) А È В; б) А Ç В; в) В \ А;г) А \ В; д) А ∆ В. 2. Даны два множества: А = {1, 4} и B = {2, 3, 5, 6}. Найти декартово произведение: а) А ´ В; б) В ´ А. 3. Даны три множества: А - множество натуральных чисел, делящихся нацело на 6; B - множество натуральных чисел, делящихся нацело на 10; С - множество натуральных чисел, делящихся нацело на 21. Определить, принадлежит ли число s = 126 множеству D = (А \ В) È (А Ç C) È (B Ç C)? Показать это число на диаграмме Венна, иллюстрирующей множество D. 4. Из 220 студентов 163 играют в баскетбол, 175 - в футбол, 24 не играют в эти игры. Сколько человек одновременно играет в баскетбол и футбол? 5. Если N – множество натуральных чисел, М - множество положительных чисел, Р - множество простых чисел, Q - множество положительных нечётных чисел. Указать истинность высказываний: а) 6. Даны два множества: А = {3 k + 3½ k = 0, 1, 2,…} и B = { m + 2½ m = 0, 1, 2,…}. Установите, является ли соответствие f: A ® B, заданное формулой 7. Найти область определения функции 8. Найти предел функции 9. Правильно ли рассуждение, имеющее форму: «Ни одно х не является у и некоторые у являются z; значит, некоторые z не являются x»? 10. Построить таблицу истинности для высказывания
11. Доказать методом математической индукции, что при любом натуральном п справедливо следующее равенство:
12. Найти обратную подстановку произведения (АВС)-1 при А = 13. Найдите производную функции 14. Вычислите интеграл 15. Переведите с точностью до 5 знаков после запятой число 23,81(10) в двоичную, восьмеричную и шестнадцатеричную систему.
Вариант 4 1. Даны два множества: А = {6 k + 5½ k = 0, 1, 2,…} и B = {3 m + 2½ m = 0, 1, 2,…}. Найти: а) А È В; б) А Ç В; в) В \ А;г) А \ В; д) А ∆ В. 2. Даны два множества: А = {3, 5} и B = {2, 4, 6,7}. Найти декартово произведение: а) А ´ В; б) В ´ А. 3. Даны три множества: А - множество натуральных чисел, делящихся нацело на 6; B - множество натуральных чисел, делящихся нацело на 10; С - множество натуральных чисел, делящихся нацело на 21. Определить, принадлежит ли число s = 210 множеству D = (А \ В) È (А Ç C) È (B Ç C)? Показать это число на диаграмме Венна, иллюстрирующей множество D. 4. В группе 30 студентов. Все, кроме трёх, по итогам экзаменационной сессии имеют оценки «удовлетворительно» («3»), «хорошо» («4») и «отлично» («5»). Число студентов, имеющих оценки «5» - одиннадцать, «4» - четырнадцать, «3» - семнадцать. Трое учатся лишь на «5» и «3», трое – лишь на «5» и «4» и четверо – лишь на «4» и на «3». Сколько студентов сдали экзаменационную сессию только на «3»? 5. Если N – множество натуральных чисел, М - множество положительных чисел, Р - множество простых чисел, Q - множество положительных нечётных чисел. Указать истинность высказываний: а) 6. Даны два множества: А = {6 k + 5½ k = 0, 1, 2,…} и B = {3 m + 2½ m = 0, 1, 2,…}. Установите, является ли соответствие f: A ® B, заданное формулой 7. Найти область определения функции 8. Найти предел функции 9. Правильно ли рассуждение, имеющее форму: «Некоторые х являются у и некоторые у являются z; значит, некоторые z не являются x»? 10. Построить таблицу истинности для высказывания
11. Доказать методом математической индукции, что при любом натуральном п справедливо следующее равенство:
12. Найти обратную подстановку произведения (АВС)-1 при А = 13. Найдите производную функции 14. Вычислите интеграл 15. Переведите с точностью до 5 знаков после запятой число 24,26(10) в двоичную, восьмеричную и шестнадцатеричную систему.
Вариант 5 1. Даны два множества: А = {2 k ½ k = 0, 1, 2,…} и B = { m + 2½ m = 0, 1, 2,…}. Найти: а) А È В; б) А Ç В; в) В \ А;г) А \ В; д) А ∆ В. 2. Даны два множества: А = {1, 5} и B = {2, 3, 4, 6}. Найти декартово произведение: а) А ´ В; б) В ´ А. 3. Даны три множества: А - множество натуральных чисел, делящихся нацело на 6; B - множество натуральных чисел, делящихся нацело на 10; С - множество натуральных чисел, делящихся нацело на 21. Определить, принадлежит ли число s = 280 множеству D = (А \ В) È (А Ç C) È (B Ç C)? Показать это число на диаграмме Венна, иллюстрирующей множество D. 4. В группе 30 студентов. Все, кроме двух, по итогам экзаменационной сессии имеют оценки «удовлетворительно» («3»), «хорошо» («4») и «отлично» («5»). Число студентов, имеющих оценки «5» - двенадцать, «4» - четырнадцать, «3» - шестнадцать. Трое учатся лишь на «5» и «3», трое – лишь на «5» и «4» и четверо – лишь на «4» и на «3». Сколько студентов имеют одновременно оценки «5», «4» и «3»? 5. Если N – множество натуральных чисел, М - множество положительных чисел, Р - множество простых чисел, Q - множество положительных нечётных чисел. Указать истинность высказываний: а) 6. Даны два множества: А = {2 k ½ k = 0, 1, 2,…} и B = { m + 2½ m = 0, 1, 2,…}. Установите, является ли соответствие f: A ® B, заданное формулой 7. Найти область определения функции 8. Найти предел функции 9. Правильно ли рассуждение, имеющее форму: «Если некоторые у являются х, некоторые у являются z и некоторые z являются х, то некоторые х одновременно являются и у, и z»? 10. Построить таблицу истинности для высказывания
11. Доказать методом математической индукции, что при любом натуральном п справедливо следующее равенство:
12. Найти обратную подстановку произведения (АВС)-1 при А = 13. Найдите производную функции 14. Вычислите интеграл 15. Переведите с точностью до 5 знаков после запятой число 15,34(10) в двоичную, восьмеричную и шестнадцатеричную систему.
Вариант 6 1. Даны два множества: А = {4 k + 1½ k = 0, 1, 2,…} и B = {3 m + 5½ m = 0, 1, 2,…}. Найти: а) А È В; б) А Ç В; в) В \ А;г) А \ В; д) А ∆ В. 2. Даны два множества: А = {1, 3, 4} и B = {2, 4, 5}. Найти декартово произведение: а) А ´ В; б) В ´ А. 3. Даны три множества: А - множество натуральных чисел, делящихся нацело на 6; B - множество натуральных чисел, делящихся нацело на 10; С - множество натуральных чисел, делящихся нацело на 21. Определить, принадлежит ли число s = 315 множеству D = (А \ В) È (А Ç C) È (B Ç C)? Показать это число на диаграмме Венна, иллюстрирующей множество D. 4. В группе 30 студентов. Все, кроме трёх, по итогам экзаменационной сессии имеют оценки «удовлетворительно» («3»), «хорошо» («4») и «отлично» («5»). Число студентов, имеющих оценки «5» - двенадцать, «4» - тринадцать, «3» - шестнадцать. Трое учатся лишь на «5» и «3», трое – лишь на «5» и «4» и четверо – лишь на «4» и на «3». Сколько студентов сдали экзаменационную сессию только на «4»? 5. Если N – множество натуральных чисел, М - множество положительных чисел, Р - множество простых чисел, Q - множество положительных нечётных чисел. Указать истинность высказываний: а) 6. Даны два множества: А = {4 k + 1½ k = 0, 1, 2,…} и B = {3 m + 5½ m = 0, 1, 2,…}. Установите, является ли соответствие f: A ® B, заданное формулой 7. Найти область определения функции 8. Найти предел функции 9. Правильно ли рассуждение, имеющее форму: «Если все у являются х, некоторые у являются z и некоторые z являются х, то некоторые х одновременно являются и у, и z»? 10. Построить таблицу истинности для высказывания
11. Доказать методом математической индукции, что при любом натуральном п справедливо следующее равенство:
12. Найти обратную подстановку произведения (АВС)-1 при А = 13. Найдите производную функции 14. Вычислите интеграл 15. Переведите с точностью до 5 знаков после запятой число 26,17(10) в двоичную, восьмеричную и шестнадцатеричную систему.
Вариант 7 1. Даны два множества: А = {2 k + 3½ k = 0, 1, 2,…} и B = {3 m ½ m = 0, 1, 2,…}. Найти: а) А È В; б) А Ç В; в) В \ А;г) А \ В; д) А ∆ В. 2. Даны два множества: А = {2, 3, 5} и B = {2, 4, 6}. Найти декартово произведение: а) А ´ В; б) В ´ А. 3. Даны три множества: А - множество натуральных чисел, делящихся нацело на 6; B - множество натуральных чисел, делящихся нацело на 10; С - множество натуральных чисел, делящихся нацело на 21. Определить, принадлежит ли число s = 390 множеству D = (А \ В) È (А Ç C) È (B Ç C)? Показать это число на диаграмме Венна, иллюстрирующей множество D. 4. Из 64 студентов на вопрос, занимаются ли они в свободное время спортом, утвердительно ответили 40 человек; на вопрос, любят ли они слушать музыку, 30 человек ответили утвердительно. Причём 21 студент занимаются спортом и любят слушать музыку. Сколько человек не увлекается ни спортом, ни музыкой? 5. Если N – множество натуральных чисел, М - множество положительных чисел, Р - множество простых чисел, Q - множество положительных нечётных чисел. Указать истинность высказываний: а) 6. Даны два множества: А = {2 k + 3½ k = 0, 1, 2,…} и B = {3 m ½ m = 0, 1, 2,…}. Установите, является ли соответствие f: A ® B, заданное формулой 7. Найти область определения функции 8. Найти предел функции 9. Правильно ли рассуждение, имеющее форму: «Все х являются у и некоторые х являются z; значит, все у являются z»? 10. Построить таблицу истинности для высказывания
11. Числовая последовательность а 0, а 1, а 2, …, ап, … определяется следующими условиями: а 0 = 1, ап +1 = 2× ап + 1. Доказать методом математической индукции, что ап = 2 n +1 – 1 при всех натуральных п. 12. Найти обратную подстановку произведения (АВС)-1 при А = 13. Найдите производную функции 14. Вычислите интеграл 15. Переведите с точностью до 5 знаков после запятой число 17,84(10) в двоичную, восьмеричную и шестнадцатеричную систему.
Вариант 8 1. Даны два множества: А = {3 k + 4½ k = 0, 1, 2,…} и B = { m + 4½ m = 0, 1, 2,…}. Найти: а) А È В; б) А Ç В; в) В \ А;г) А \ В; д) А ∆ В. 2. Даны два множества: А = {3, 5} и B = {1, 2, 5, 6}. Найти декартово произведение: а) А ´ В; б) В ´ А. 3. Даны три множества: А - множество натуральных чисел, делящихся нацело на 6; B - множество натуральных чисел, делящихся нацело на 10; С - множество натуральных чисел, делящихся нацело на 21. Определить, принадлежит ли число s = 420 множеству D = (А \ В) È (А Ç C) È (B Ç C)? Показать это число на диаграмме Венна, иллюстрирующей множество D. 4. Из 20 студентов двое могут играть только в шахматы, трое – только в шашки, шестеро – только в футбол. Никто не умеет играть во все три игры. Один играет в шахматы и шашки, трое - в футбол и шахматы. Сколько студентов умеет играть в футбол и шашки? 5. Если N – множество натуральных чисел, М - множество положительных чисел, Р - множество простых чисел, Q - множество положительных нечётных чисел. Указать истинность высказываний: а) 6. Даны два множества: А = {3 k + 4½ k = 0, 1, 2,…} и B = { m + 4½ m = 0, 1, 2,…}. Установите, является ли соответствие f: A ® B, заданное формулой 7. Найти область определения функции 8. Найти предел функции 9. Правильно ли рассуждение, имеющее форму: «Некоторые х являются у и все х являются z; значит, некоторые у являются z»? 10. Построить таблицу истинности для высказывания
11. Числовая последовательность а 1, а 2, …, ап, … определяется следующими условиями: а 1 = 2, ап +1 = 3× ап + 1. Доказать методом математической индукции, что ап = 12. Найти обратную подстановку произведения (АВС)-1 при А = 13. Найдите производную функции 14. Вычислите интеграл 15. Переведите с точностью до 5 знаков после запятой число 18,37(10) в двоичную, восьмеричную и шестнадцатеричную систему.
Вариант 9 1. Даны два множества: А = {5 k + 1½ k = 0, 1, 2,…} и B = { m + 1½ m = 0, 1, 2,…}. Найти: а) А È В; б) А Ç В; в) В \ А;г) А \ В; д) А ∆ В. 2. Даны два множества: А = {1, 3, 7} и B = {4, 5, 6}. Найти декартово произведение: а) А ´ В; б) В ´ А. 3. Даны три множества: А - множество натуральных чисел, делящихся нацело на 6; B - множество натуральных чисел, делящихся нацело на 10; С - множество натуральных чисел, делящихся нацело на 21. Определить, принадлежит ли число s = 504 множеству D = (А \ В) È (А Ç C) È (B Ç C)? Показать это число на диаграмме Венна, иллюстрирующей множество D. 4. Среди 35 студентов одним английским языком владеют 11 человек, английским и французским – 5 человек. Не владеют ни английским, ни французским 9 человек. Сколько студентов владеет французским языком? 5. Если N – множество натуральных чисел, М - множество положительных чисел, Р - множество простых чисел, Q - множество положительных нечётных чисел. Указать истинность высказываний: а) М = 6. Даны два множества: А = {5 k + 1½ k = 0, 1, 2,…} и B = { m + 1½ m = 0, 1, 2,…}. Установите, является ли соответствие f: A ® B, заданное формулой 7. Найти область определения функции 8. Найти предел функции 9. Правильно ли рассуждение, имеющее форму: «Все х являются у и некоторые у являются z; значит, все z не являются х»? 10. Построить таблицу истинности для высказывания
11. Числовая последовательность а 0, а 1, а 2, …, ап, … определяется следующими условиями: а 0 = 2, а 1 = 3, ап +1 = a 1 × ап – а 0 × ап -1. Доказать методом математической индукции, что ап = 2 n + 1 при всех натуральных п. 12. Найти обратную подстановку произведения (АВС)-1 при А = 13. Найдите производную функции 14. Вычислите интеграл 15. Переведите с точностью до 5 знаков после запятой число 29,26(10) в двоичную, восьмеричную и шестнадцатеричную систему.
Вариант 10 1. Даны два множества: А = { k + 3½ k = 0, 1, 2,…} и B = { m + 2½ m = 0, 1, 2,…}. Найти: а) А È В; б) А Ç В; в) В \ А;г) А \ В; д) А ∆ В. 2. Даны два множества: А = {7, 8} и B = {2, 4, 5, 6}. Найти декартово произведение: а) А ´ В; б) В ´ А. 3. Даны три множества: А - множество натуральных чисел, делящихся нацело на 6; B - множество натуральных чисел, делящихся нацело на 10; С - множество натуральных чисел, делящихся нацело на 21. Определить, принадлежит ли число s = 630 множеству D = (А \ В) È (А Ç C) È (B Ç C)? Показать это число на диаграмме Венна, иллюстрирующей множество D. 4. В группе 30 студентов. Все, кроме двух, по итогам экзаменационной сессии имеют оценки «удовлетворительно» («3»), «хорошо» («4») и «отлично» («5»). Число студентов, имеющих оценки «5» - двенадцать, «4» - четырнадцать, «3» - шестнадцать. Двое учатся одновременно на «5», «4» и «3», трое – лишь на «5» и «4» и четверо – лишь на «4» и на «3». Сколько студентов имеет только оценки «5» и «3»? 5. Если N – множество натуральных чисел, М - множество положительных чисел, Р - множество простых чисел, Q - множество положительных нечётных чисел. Указать истинность высказываний: а) М = 6. Даны два множества: А = { k + 3½ k = 0, 1, 2,…} и B = { m + 2½ m = 0, 1, 2,…}. Установите, является ли соответствие f: A ® B, заданное формулой 7. Найти область определения функции 8. Найти предел функции 9. Правильно ли рассуждение, имеющее форму: «Все х являются у и все у являются z; значит, некоторые z являются х»? 10. Построить таблицу истинности для высказывания
11. Доказать методом математической индукции, что неравенство 12. Найти обратную подстановку произведения (АВС)-1 при А = 13. Найдите производную функции 14. Вычислите интеграл 15. Переведите с точностью до 5 знаков после запятой число 15,18(10) в двоичную, восьмеричную и шестнадцатеричную систему. Методические рекомендации по выполнению контрольной работы по разделу «Математика»
При подготовке контрольной работы по разделу «Математика» необходимо придерживаться следующих рекомендаций. Во-первых, можно пользоваться любыми доступными изданиями по высшей математике, раскрывающими соответствующие темы. Список рекомендуемой литературы приведён в приложении 4. Во-вторых, о логике изложения. Решение задач должно быть логически стройным, т.е. содержать однозначную минимальную последовательность операций, обеспечивающую получение для заданных исходных данных искомого результата. Сопутствующие сведения, затрудняющие понимание главного, опускаются. Это в равной мере относится как к тексту, так и к иллюстрациям. В-третьих, о способе решения. Большая часть задач контрольной работы по разделу «Математика» (№№ 1, 3, 4, 5, 6, 9) ориентирована на использование математического аппарата теории множеств. Поэтому будет уместной иллюстрация решения таких задач с помощью диаграмм Венна. Проиллюстрируем эту рекомендацию примером выполнения задач данного типа. Задача 1. Даны два множества: А = {6 k + 5ï k = 0, 1, 2, …} и B = {3 m + 2 ï m = 0, 1, 2, …}. Найти: а) А È В; б) А Ç В; в) В \ А; г) А \ В; д) A ∆ B. Решение Определим, какие элементы принадлежат множествам: А = {5, 11, 17, 23, 29, …}; B = {2, 5, 8, 11, 14, 17, …}. Проиллюстрируем данные множества с помощью диаграмм Венна:
Найдём объединение, пересечение, разность и симметрическую разность множеств: а) А È В = В; б) А Ç В = А; в) В \ А = {2, 8, 14, 20, … } = {6 k + 2 ï k = 0, 1, 2, …}; г) А \ В = Æ; д) A ∆ B = {2, 8, 14, 20, …} = {6 k + 2 ï k = 0, 1, 2, …}. Задача 3. Даны три множества: А - множество натуральных чисел, делящихся нацело на 6; B - множество натуральных чисел, делящихся нацело на 10; С - множество натуральных чисел, делящихся нацело на 21. Определить, принадлежит ли число s = 420 множеству D = (А \ В) È (А Ç C) È (B Ç C)? Показать это число на диаграмме Венна, иллюстрирующей множество D. Решение Определив делимость числа 420 на 6, 10, 21, установим его принадлежность заданным множествам: 420 Î А, 420 Î В, 420 Î С. Отметив факт принадлежности числа множеству знаком «+», заполним табл. 1. Результат - в последнем столбце первой строки табл. 1. Таблица 1
Из диаграммы Венна (рис. 1) заключаем, что множество D изображается объединением заштрихованных областей, а число 420 принадлежит области пересечения множеств А, В и С.
Рис. 1 Задача 4. Из 20 студентов двое могут играть только в шахматы, трое – только в шашки, шестеро – только в футбол. Никто не умеет играть во все три игры. Один играет в шахматы и шашки, трое - в футбол и шахматы. Сколько студентов умеют играть в футбол и шашки? Решение Обозначим через А множество студентов, играющих в шахматы, через В - в шашки, через С - в футбол. По условию задачи: | А È В È С | = 20, | А Ç В | = 1, | А Ç С | =3, А Ç В Ç С = = Æ (никто не умеет играть сразу в три игры). Требуется определить количество элементов в пересечении В Ç С. Изобразим эти множества на диаграмме Венна (рис. 2). Из диаграммы видно, что множество В Ç С должно содержать 20 – 1 – 2 – 3 – 6 – 3 = 5. Значит, играть в футбол и шашки умеют 5 студентов.
Рис. 2 Задача 5. Если N – множество натуральных чисел, М - множество положительных чисел, Р - множество простых чисел, Q - множество положительных нечётных чисел. Указать истинность высказываний: а) Решение Для указанных множеств справедливо:
Тогда а) б) в) г) Задача 6. Даны два множества: А = {2 k ï k = 0, 1, 2, …} и B = {2 m + 1ï m = 0, 1, …}. Установите, является ли соответствие f: A ® B, заданное формулой b = a +1, взаимно однозначным. Решение
Задача 9. Правильно ли рассуждение, имеющее форму: «Все х являются у и ни одно х не является z; значит, все у не являются z»? Решение Построим диаграммы Венна, характеризующие посылки и заключение:
В-четвёртых, об использовании определений. Решение задач № 2 и № 7 предполагает практическую иллюстрацию терминов «декартово произведение множеств» и «область определения функции». Приведём соответствующие примеры. Задача 2. Даны два множества: А = {1, 2} и B = {4, 7, 8}. Найти декартово произведение: а) А ´ В; б) В ´ А. Решение Декартовым (или прямым) произведением А ´ В двух множеств А и В называется множество всех упорядоченных пар (a, b), где а Î А, b Î В. Тогда А ´ В = {(1, 4), (1, 7), (1, 8), (2, 4), (2, 7), (2, 8)}; В ´ А = {(4, 1), (4, 2), (7, 1), (7, 2), (8, 1), (8, 2)}. Задача 7. Найти область определения функции Решение Под областью определения функции подразумевается естественная область определения, т.е. те значения х &
|

 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. , взаимно однозначным.
, взаимно однозначным. .
.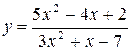 при х ® ¥.
при х ® ¥. .
. .
. В =
В =  С =
С =  .
. .
. .
. ; б)
; б)  ; в)
; в) 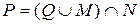 ; г)
; г)  .
.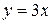 , взаимно однозначным.
, взаимно однозначным. .
. при х ® ¥.
при х ® ¥.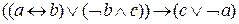 .
. .
. В =
В =  С =
С =  .
. .
. .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. , взаимно однозначным.
, взаимно однозначным. .
. при х ® ¥.
при х ® ¥. .
. .
. .
.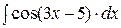 .
. ; б)
; б)  ; в)
; в) 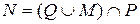 ; г)
; г)  .
. , взаимно однозначным.
, взаимно однозначным. .
. при х ® ¥.
при х ® ¥. .
.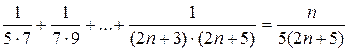 .
. .
. .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. , взаимно однозначным.
, взаимно однозначным. .
. при х ® ¥.
при х ® ¥. .
. .
. .
. .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. , взаимно однозначным.
, взаимно однозначным.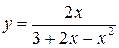 .
. при х ® ¥.
при х ® ¥. .
. .
.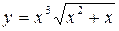 .
. .
.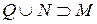 ; б)
; б)  ; в)
; в)  ; г)
; г) 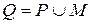 .
. .
. при х ® 0.
при х ® 0. .
. В =
В = 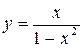 .
. .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. , взаимно однозначным.
, взаимно однозначным. .
. при х ® 0.
при х ® 0. .
. (5×3 n -1 – 1) при всех натуральных п.
(5×3 n -1 – 1) при всех натуральных п. .
. .
. ; б) Р =
; б) Р =  ; в)
; в)  ; г)
; г)  .
. , взаимно однозначным.
, взаимно однозначным. .
. при х ® 0.
при х ® 0. .
.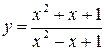 .
. .
.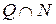 ; б) Р =
; б) Р =  ; в)
; в)  ; г)
; г)  .
. , взаимно однозначным.
, взаимно однозначным. .
. при х ® 0.
при х ® 0. .
. выполняется при всех натуральных п > 3.
выполняется при всех натуральных п > 3. .
. .
.
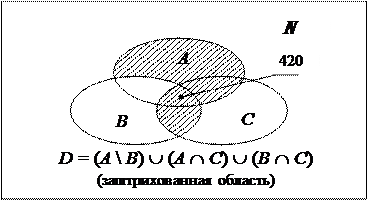

 ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. ,
,  Графическая иллюстрация:
Графическая иллюстрация:
 ,
,  , т.е. ложно;
, т.е. ложно; ,
,  , т.е. истинно;
, т.е. истинно; ,
, 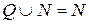 ,
,  , т.е. ложно;
, т.е. ложно; ,
,  , т.е. ложно.
, т.е. ложно. Проиллюстрируем возможность установления взаимного однозначного соответствия:
Проиллюстрируем возможность установления взаимного однозначного соответствия: Из рис. видно, что возможно неверное заключение, удовлетворяющее исходным посылкам. Следовательно, рассуждение не является правильным.
Из рис. видно, что возможно неверное заключение, удовлетворяющее исходным посылкам. Следовательно, рассуждение не является правильным. .
.


