Основные законы и формулы. · Скорость света в среде
· Скорость света в среде
где с – скорость света в вакууме; n – показатель преломления среды (абсолютный). · Оптическая длина пути, проходимого световым лучом в однородной среде с показателем преломления n
где l – геометрическая длина пути световой волны. · Оптическая разность хода двух световых волн (лучей)
· Условие максимального усиления света при интерференции (интерференционный максимум)
где λ0 – длина световой волны в вакууме. Условие максимального ослабления света (интерференционный минимум)
· Условия дифракционных максимумов и минимумов от одной щели
где а – ширина щели; k – порядковый номер; j – угол дифракции. · Условие главных максимумов дифракционной решётки
где d – постоянная (период) дифракционной решётки, j – угол дифракции. · Разрешающая способность (сила) дифракционной решётки
где D l – наименьшая разность длин волн двух соседних спектральных линий (l и l +D l), при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решетки; N – полное число щелей решётки; k – порядок спектра. · Степень поляризации света
где I max и I min – максимальная и минимальная интенсивности света, соответствующие двум взаимно перпендикулярным направлениям световых колебаний в луче. · Закон Брюстера tg iB = где i – угол падения, при котором отразившийся от границы раздела двух диэлектриков луч полностью поляризован; n 21 – относительный показатель преломления второй среды относительно первой. · Закон Малюса
где I 0 – интенсивность плоскополяризованного света, падающего на анализатор; I – интенсивность этого света после анализатора; α; – угол между главными плоскостями поляризации (пропускания) поляризатора и анализатора. · Закон Стефана – Больцмана
где Re – энергетическая светимость (излучательность) абсолютно чёрного тела; s – постоянная Стефана – Больцмана. · Закон смещения Вина:
где λmax – длина волны, на которую приходится максимум энергии излучения; b = 2,9·10-3 м·К – постоянная смещения Вина. · Второй закон Вина: максимальное значение спектральной плотности энергетической светимости
где С = 1,29×10-5 · Энергия фотона
где n – частота фотона. · Масса фотона
где с – скорость света в вакууме; λ; – длина волны фотона. · Импульс фотона
· Уравнение Эйнштейна для внешнего фотоэффекта
где hv – энергия фотона, падающего на поверхность металла; А – работа выхода электрона; Т – максимальная кинетическая энергия фотоэлектрона. · Красная граница фотоэффекта
где
· Давление света при нормальном падении на поверхность
где Ее – энергетическая освещенность (облученность) поверхности; w – объемная плотность энергии излучения; с – скорость света в вакууме; r – коэффициент отражения. · Изменение длины волны при эффекте Комптона
где λ;1 – длина волны падающего фотона; λ;2 – длина волны рассеянного фотона; θ; – угол рассеяния фотона после столкновения с частицей; m0 – масса покоящейся частицы.
· Первый постулат Бора. Электрон в атоме водорода движется, не излучая, по круговой орбите, для которой момент импульса электрона
где me – масса электрона;
rn – радиус n -ой стационарной орбиты; ħ = 1,05×10-34 Дж×с, или h = 6,63×10-34 Дж×с – постоянная Планка; n = 1, 2, 3,… – квантовое число (номер орбиты электрона). · Второй постулат Бора. При переходе электрона с одной орбиты на другую атом водорода излучает или поглощает квант энергии:
где · Полная энергия электрона в атоме водорода
где n – номер орбиты; me – масса электрона; е – заряд электрона; ε0 = 8,85×10-12 Ф/м – электрическая постоянная; h – постоянная Планка.
· Формула, позволяющая найти частоты v или длины волн λ, соответствующие линиям водородного спектра (сериальная формула Бальмера)
где R – постоянная Ридберга (R = 1,10×107 м-1); с – скорость света в вакууме; n1 и n2 – квантовые числа, определяющие номера орбит электрона. Для водородоподобных ионов формула имеет вид:
где Z – порядковый номер в таблице Менделеева. · Длина волны де Бройля
где p=m · Импульс частицы и его связь с кинетической энергией T: а) б) где m 0 – масса покоя частицы; m – релятивистская масса частицы;
с – скорость света в вакууме; Е 0 – энергия покоя частицы (Е 0 = m 0 с2). · Соотношение неопределенностей: а) для координаты и импульса
где D Рх – неопределенность проекции импульса на ось Х; D х – неопределенность координаты; б) для энергии и времени
где D Е – неопределенность энергии; D t – неопределенность времени жизни квантовой системы в данном энергетическом состоянии.
· Закон радиоактивного распада
где N – число ядер, не распавшихся к моменту времени t; N 0 – число ядер в начальный момент (t = 0); λ; – постоянная радиоактивного распада. · Период полураспада
· Среднее время жизни радиоактивного ядра, т.е. интервал времени, за который число нераспавшихся ядер уменьшилось в е раз:
· Число атомов, содержащихся в радиоактивном изотопе
где m – масса изотопа; М – молярная масса; NA – постоянная Авогадро (NA =6,02×1023 моль-1). · Активность радиоактивного изотопа
где А 0 – активность изотопа в начальный момент времени (t = 0), А 0 =λN 0. · Дефект массы ядра
где Z – зарядовое число (число протонов в ядре); А – массовое число (число нуклонов в ядре); (А-Ζ;) – число нейтронов в ядре; mр – масса протона; mn – масса нейтрона; mя – масса ядра. · Энергия связи ядра Есв = D mс2, где Δ m – дефект массы ядра; с – скорость света в вакууме. Во внесистемных единицах энергия связи ядра равна Есв = 931×Δ m Мэв, где дефект массы Δ m – в а.е.м.; 931 – коэффициент пропорциональности (1 а.е.м. ~ 931 МэВ). · Правило смещения: 1) для α; -распада: 2) для β- -распада: 3) для β+ -распада: · Ядерные реакции. Символическая запись ядерной реакции может быть дана или в развернутом виде, например:
или сокращенно
При сокращенной записи порядковый номер атома не пишут, так как он определяется химическим символом атома. В скобках на первом месте ставят обозначение бомбардирующей частицы, на втором – обозначение частицы, вылетающей из составного ядра, и за скобками – химический символ ядра-продукта. Обозначения частиц: р – протон, n – нейрон, d – дейтрон, t – тритий (тритон), α; -альфа-частица, γ-гамма-фотон. · Энергетический эффект ядерной реакции Q = c 2[(m 1 +m 2) –(m 3 +m 4)], где m 1 – масса покоя ядра-мишени; m 2 – масса покоя бомбардирующей частицы, (m 3 + m 4) – сумма масс покоя ядер продуктов реакции. Если m 1 + m 2 > m 3 + m 4, то энергия освобождается, реакция экзотермическая. Если m 1 + m 2 < m 3 + m 4, то энергия поглощается, реакция эндотермическая. · При решении задач на ядерные реакции применяются законы сохранения: 1) электрического заряда: z 1 + z 2 = z 3 + z 4; 2) суммарного числа нуклонов: А 1 + А 2 = А 3 + А 4; 3) релятивистской полной энергии: Е 1 + Е 2 = Е 3 + Е 4; или
где 4) импульса: р 1 + р 2 = р 3 + р 4.
|


 ,
, .
. (k =0,1,2,3,…),
(k =0,1,2,3,…),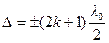 (k =0,1,2,3,…).
(k =0,1,2,3,…).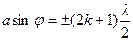 (k =1,2,3…);
(k =1,2,3…); (k =1,2,3…),
(k =1,2,3…), (k =1,2,3…),
(k =1,2,3…), ,
, ,
,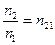 ,
,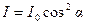 ,
,
 ,
, абсолютно черного тела пропорционально пятой степени абсолютной температуры
абсолютно черного тела пропорционально пятой степени абсолютной температуры ,
, – постоянная Вина.
– постоянная Вина. ,
,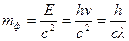 ,
, .
. ,
, , или
, или  ,
, – минимальная частота света, при которой еще возможен фотоэффект;
– минимальная частота света, при которой еще возможен фотоэффект; – максимальная длина волны света, начиная с которой фотоэффект прекращается.
– максимальная длина волны света, начиная с которой фотоэффект прекращается. ,
, ,
,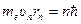 , или
, или  ,
, – скорость электрона на n -ой орбите;
– скорость электрона на n -ой орбите; ,
, и
и  – полные энергии электрона в атоме на соответствующей орбите.
– полные энергии электрона в атоме на соответствующей орбите. (n = 1, 2, 3,…),
(n = 1, 2, 3,…), ,
, ,
, ,
, – модуль импульса движущейся частицы.
– модуль импульса движущейся частицы. ;
;  ;
; ;
; 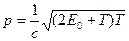 ,
, ,
, ,
, ,
, .
. .
. ,
, ,
, ,
, ;
; ;
; .
.
 .
. ,
, – сумма энергий покоя частиц и их кинетических энергий до реакции; справа то же для частиц после реакции;
– сумма энергий покоя частиц и их кинетических энергий до реакции; справа то же для частиц после реакции;


