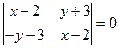4.1. Найти косинус угла 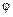 , образованного вектором
, образованного вектором  и ортом
и ортом  оси
оси 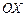 , если
, если 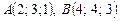 . Найти
. Найти 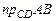 , если
, если 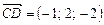 .
.
4.2.Найти 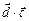 , если
, если 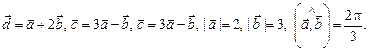
4.3.Найти направляющие косинусы вектора  , если
, если 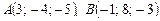 .
.
4.4.Вектор 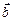 параллелен вектору
параллелен вектору  и образует с осью
и образует с осью 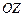 острый угол. Зная, что
острый угол. Зная, что 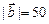 , найти координаты вектора
, найти координаты вектора 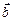 .
.
4.5.Найти вектор, параллельный вектору 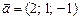 и удовлетворяющий условию
и удовлетворяющий условию  .
.
4.6.Даны два вектора 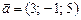 и
и 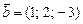 . Найти вектор
. Найти вектор 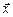 , при условии, что он ортогонален оси
, при условии, что он ортогонален оси 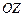 и
и  .
.
4.7.Найти длину диагоналей параллелограмма, построенного на векторах  и
и  , если известно, что
, если известно, что 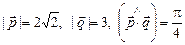 .
.
4.8.Даны три последовательных вершины параллелограмма  . Найти его четвертую вершину
. Найти его четвертую вершину  и угол между векторами
и угол между векторами  и
и 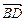 .
.
4.9.Найти угол между векторами 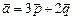 и
и 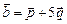 , где
, где 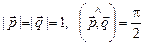 .
.
4.10. Дано 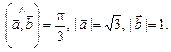 Найти угол меду векторами
Найти угол меду векторами  и
и  .
.
4.11.Дано  При каком значении
При каком значении  вектор
вектор 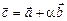 и
и 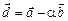 ортогональны.
ортогональны.
4.12.аны векторы 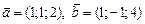 . Найти
. Найти 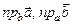 и
и 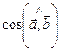 .
.
4.13.Даны векторы 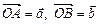 , для которых
, для которых 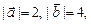
 . Вычислить угол
. Вычислить угол 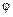 между медианой
между медианой  и стороной
и стороной  треугольника
треугольника  .
.
4.14.Даны вершины четырёхугольника 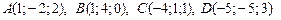 . Вычислить угол
. Вычислить угол 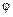 между его диагоналями.
между его диагоналями.
4.15.Зная векторы, совпадающие с двумя сторонами треугольника  , Найти внутренние углы треугольника.
, Найти внутренние углы треугольника.
4.16. Найти единичный вектор 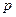 , одновременно перпендикулярный к вектору
, одновременно перпендикулярный к вектору  и оси
и оси  .
.
4.17. На векторах  и
и 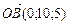 построен
построен  . Точка М делит сторону АВ в отношении 2:3. Найти координаты вектора
. Точка М делит сторону АВ в отношении 2:3. Найти координаты вектора  .
.
4.18. Векторы 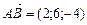 и
и  совпадают со сторонами треугольника
совпадают со сторонами треугольника 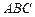 . Определить координаты векторов, совпадающих с его медианами
. Определить координаты векторов, совпадающих с его медианами 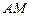 ,
,  и
и  .
.
4.19. Зная векторы, совпадающие с двумя сторонами треугольника  и
и 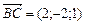 , найти внутренние углы треугольника.
, найти внутренние углы треугольника.
4.20. Вектор 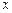 , перпендикулярный к векторам
, перпендикулярный к векторам  и
и  , образует с осью
, образует с осью  тупой угол. Найти его координаты, если
тупой угол. Найти его координаты, если 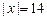 .
.
4.21. Найти углы треугольника 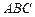 с вершинами
с вершинами 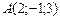 ,
,  и
и  .
.
4.22. Векторы 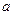 и
и 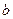 образуют угол
образуют угол  ,
, 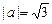 ,
, 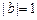 . Вычислить угол
. Вычислить угол 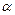 между векторами
между векторами  и
и 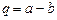 .
.
4.23. Найти вектор  , если известно, что он коллинеарны вектору
, если известно, что он коллинеарны вектору  и
и
а). А (9;-1;6), В (11;-3;7), 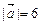 , пр Ox
, пр Ox  <0.
<0.
б). А (-1;-1;6), В (2;5;4), 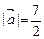 , пр Oz
, пр Oz  >0.
>0.
в). А (-2;1;4), В (-6;3;8),  , пр Oy
, пр Oy  >0.
>0.
4.24. Известно, что вектор  ортогонален векторам
ортогонален векторам 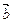 и
и 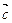 . Найти
. Найти  , если
, если
а)  ,
,  ,
, 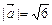 , пр Ox
, пр Ox  <0.
<0.
б) 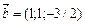 ,
,  ,
,  , пр Ox
, пр Ox  >0.
>0.
4.25. Даны три вектора  ,
,  ,
,  . Найти вектор
. Найти вектор  , удовлетворяющий условиям
, удовлетворяющий условиям  ,
, 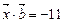 ,
,  .
.
4.26. Даны векторы 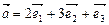 ,
,  ,
, 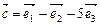 , где
, где  — базис. Доказать, что векторы
— базис. Доказать, что векторы 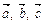 образуют базис. Найти координаты вектора
образуют базис. Найти координаты вектора 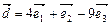 в базисе
в базисе 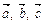 .
.
4.27. Найти скалярное произведение векторов (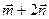 ) и (
) и (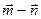 ), если
), если  ,
, 
 а угол между векторами
а угол между векторами 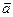 и
и 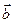 равен
равен  .
.
4.28. Зная вершину А (1;0;5) треугольника и векторы, совпадающие с двумя сторонами: 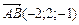 и
и 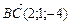 , найти координаты вершин В и С.
, найти координаты вершин В и С.
4.29. Даны вершины треугольника: А (4;-1;2), В (0;1;-3), С (6;5;3). Найти координаты вектора  , если AD — медиана.
, если AD — медиана.
4.30. Даны точки А (-1;0;2), В (2;3;-4), С (2;3;4). Найти координаты вектора  , если известно, что точка D делит отрезок ВС в отношении
, если известно, что точка D делит отрезок ВС в отношении 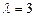 .
.
ЗАДАНИЕ № 5.
Для матриц
 найти:
найти:
5.1. 
| 5.11. 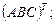
| 5.21. 
| |
5.2. 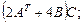
| 5.12. 
| 5.22. 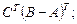
| |
5.3. 
| 5.13. 
| 5.23. 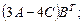
| |
5.4. 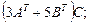
| 5.14. 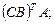
| 5.24. 
| |
5.5. 
| 5.15. 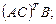
| 5.25. 
| |
5.6. 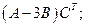
| 5.16. 
| 5.26. 
| |
5.7. 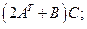
| 5.17. 
| 5.27. 
| |
5.8. 
| 5.18. 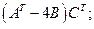
| 5.28. 
|
5.9. 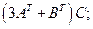
| 5.19. 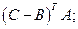
| 5.29. 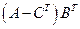
|
5.10. 
| 5.20. 
| 5.30. 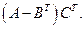
| |
ЗАДАНИЕ № 6. Найти f (A) для данных A и f (x)
6.1. A = 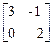 , f(x) = x3 – 2x2 + x + 4 , f(x) = x3 – 2x2 + x + 4
| 6.16. 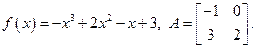
|
6.2. A =  , f(x) = 3x2 - 4x +1 , f(x) = 3x2 - 4x +1
| 6.17. 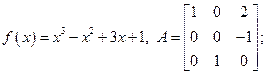
|
6.3. A =  , f(x) = x4 - 2x2 + 3x + 5 , f(x) = x4 - 2x2 + 3x + 5
| 6.18. 
|
6.4. A = 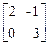 , f(x) = x2 - 5x +6 , f(x) = x2 - 5x +6
| 6.19. 
|
6.5. A = 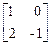 , f(x) = 2x3 - 4x2 + 3; , f(x) = 2x3 - 4x2 + 3;
| 6.20. 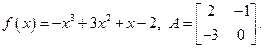
|
6.6. A =  , f(x) = x2 - 3x + 5 , f(x) = x2 - 3x + 5
| 6.21. 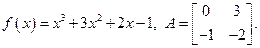
|
6.7. A =  , f(x) = – x4 +15x3 + 6x2 - 7; , f(x) = – x4 +15x3 + 6x2 - 7;
| 6.22. 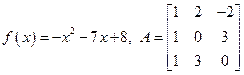
|
6.8. A = 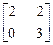 , f(x) = x2 - 5x + 6; , f(x) = x2 - 5x + 6;
| 6.23. 
|
6.9. A = 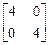 , f(x) = x3 - 3x2 + 4x - 1; , f(x) = x3 - 3x2 + 4x - 1;
| 6.24. 
|
6.10. A = 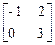 , f(x) = x3 - x2 + 5x + 4; , f(x) = x3 - x2 + 5x + 4;
| 6.25. 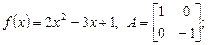
|
6.11. A =  , f(x) = x3 - 5x2 + 7x - 3 , f(x) = x3 - 5x2 + 7x - 3
| 6.26. 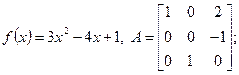
|
6.12. A = 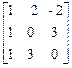 , f(x) = x3 – 5x+ 7; , f(x) = x3 – 5x+ 7;
| 6.27. 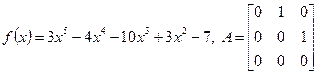
|
6.13. A = 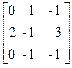 , f(x) = x2 + 1; , f(x) = x2 + 1;
| 6.28. 
|
6.14. A = 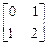 , P(x) = x2 -2x + 1; , P(x) = x2 -2x + 1;
| 6.29. 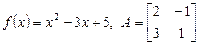
|
6.15. A = 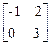 , f(x) = x2 – 3x + 1. , f(x) = x2 – 3x + 1.
| 6.30. 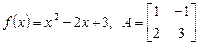
|
ЗАДАНИЕ № 7. Решить указанное уравнение либо неравенство:
7.1.  ; ;
| 7.11. 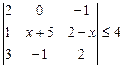 ; ;
| 7.21. 
|
7.2.  ; ;
| 7.12.  ; ;
| 7.22. 
|
7.3. 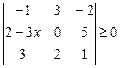 ; ;
| 7.13.  ; ;
| 7.23. 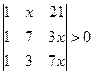
|
7.4.  ; ;
| 7.14. 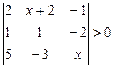 ; ;
| 7.24. 
|
7.5. 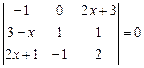 ; ;
| 7.15. 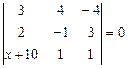 ; ;
| 7.25. 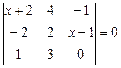
|
7.6.  ; ;
| 7.16. 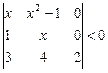
| 7.26. 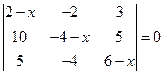
|
7.7.  ; ;
| 7.17. 
| 7.27. 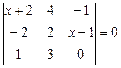
|
7.8.  ; ;
| 7.18. 
| 7.28. 
|
7.9.  ; ;
| 7.19. 
| 7.29. 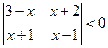
|
7.10.  ; ;
| 7.20. 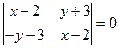
| 7.30. 
|

 , образованного вектором
, образованного вектором  и ортом
и ортом  оси
оси 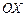 , если
, если 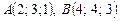 . Найти
. Найти 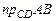 , если
, если 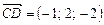 .
.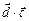 , если
, если 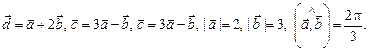
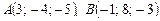 .
.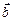 параллелен вектору
параллелен вектору  и образует с осью
и образует с осью 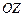 острый угол. Зная, что
острый угол. Зная, что 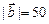 , найти координаты вектора
, найти координаты вектора 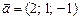 и удовлетворяющий условию
и удовлетворяющий условию  .
.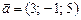 и
и 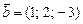 . Найти вектор
. Найти вектор 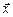 , при условии, что он ортогонален оси
, при условии, что он ортогонален оси  .
. и
и  , если известно, что
, если известно, что 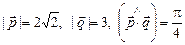 .
. . Найти его четвертую вершину
. Найти его четвертую вершину  и угол между векторами
и угол между векторами  и
и 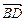 .
.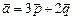 и
и 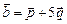 , где
, где 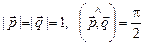 .
.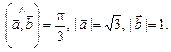 Найти угол меду векторами
Найти угол меду векторами  и
и  .
. При каком значении
При каком значении  вектор
вектор 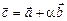 и
и 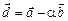 ортогональны.
ортогональны.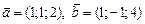 . Найти
. Найти 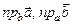 и
и 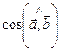 .
.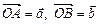 , для которых
, для которых 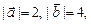
 . Вычислить угол
. Вычислить угол  и стороной
и стороной  .
.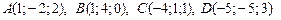 . Вычислить угол
. Вычислить угол  , Найти внутренние углы треугольника.
, Найти внутренние углы треугольника.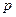 , одновременно перпендикулярный к вектору
, одновременно перпендикулярный к вектору  и оси
и оси  .
. и
и 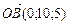 построен
построен  . Точка М делит сторону АВ в отношении 2:3. Найти координаты вектора
. Точка М делит сторону АВ в отношении 2:3. Найти координаты вектора  .
.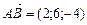 и
и  совпадают со сторонами треугольника
совпадают со сторонами треугольника 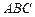 . Определить координаты векторов, совпадающих с его медианами
. Определить координаты векторов, совпадающих с его медианами 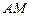 ,
,  и
и  .
. и
и 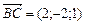 , найти внутренние углы треугольника.
, найти внутренние углы треугольника.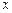 , перпендикулярный к векторам
, перпендикулярный к векторам  и
и  , образует с осью
, образует с осью  тупой угол. Найти его координаты, если
тупой угол. Найти его координаты, если 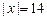 .
.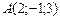 ,
,  и
и  .
.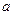 и
и 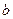 образуют угол
образуют угол  ,
, 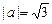 ,
, 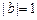 . Вычислить угол
. Вычислить угол 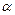 между векторами
между векторами  и
и 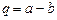 .
. , если известно, что он коллинеарны вектору
, если известно, что он коллинеарны вектору  и
и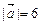 , пр Ox
, пр Ox 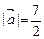 , пр Oz
, пр Oz  , пр Oy
, пр Oy 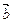 и
и 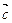 . Найти
. Найти  ,
,  ,
, 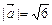 , пр Ox
, пр Ox 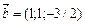 ,
,  ,
,  ,
,  ,
,  . Найти вектор
. Найти вектор  , удовлетворяющий условиям
, удовлетворяющий условиям  ,
, 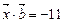 ,
,  .
.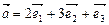 ,
,  ,
, 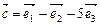 , где
, где  — базис. Доказать, что векторы
— базис. Доказать, что векторы 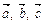 образуют базис. Найти координаты вектора
образуют базис. Найти координаты вектора 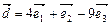 в базисе
в базисе 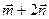 ) и (
) и (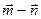 ), если
), если  ,
, 
 а угол между векторами
а угол между векторами 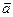 и
и 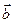 равен
равен  .
.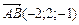 и
и 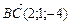 , найти координаты вершин В и С.
, найти координаты вершин В и С. , если AD — медиана.
, если AD — медиана. , если известно, что точка D делит отрезок ВС в отношении
, если известно, что точка D делит отрезок ВС в отношении 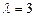 .
. найти:
найти:
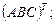

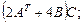

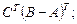


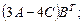
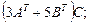
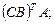


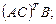

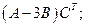


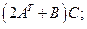



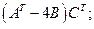

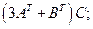
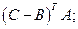
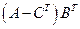


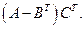
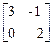 , f(x) = x3 – 2x2 + x + 4
, f(x) = x3 – 2x2 + x + 4
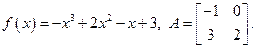
 , f(x) = 3x2 - 4x +1
, f(x) = 3x2 - 4x +1
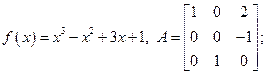
 , f(x) = x4 - 2x2 + 3x + 5
, f(x) = x4 - 2x2 + 3x + 5

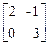 , f(x) = x2 - 5x +6
, f(x) = x2 - 5x +6

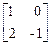 , f(x) = 2x3 - 4x2 + 3;
, f(x) = 2x3 - 4x2 + 3;
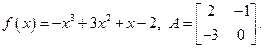
 , f(x) = x2 - 3x + 5
, f(x) = x2 - 3x + 5
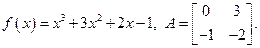
 , f(x) = – x4 +15x3 + 6x2 - 7;
, f(x) = – x4 +15x3 + 6x2 - 7;
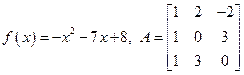
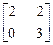 , f(x) = x2 - 5x + 6;
, f(x) = x2 - 5x + 6;

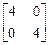 , f(x) = x3 - 3x2 + 4x - 1;
, f(x) = x3 - 3x2 + 4x - 1;

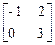 , f(x) = x3 - x2 + 5x + 4;
, f(x) = x3 - x2 + 5x + 4;
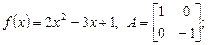
 , f(x) = x3 - 5x2 + 7x - 3
, f(x) = x3 - 5x2 + 7x - 3
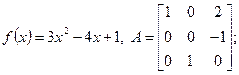
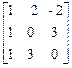 , f(x) = x3 – 5x+ 7;
, f(x) = x3 – 5x+ 7;
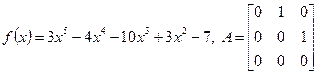
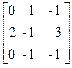 , f(x) = x2 + 1;
, f(x) = x2 + 1;

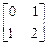 , P(x) = x2 -2x + 1;
, P(x) = x2 -2x + 1;
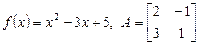
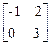 , f(x) = x2 – 3x + 1.
, f(x) = x2 – 3x + 1.
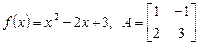
 ;
;
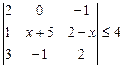 ;
;

 ;
;
 ;
;

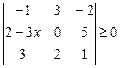 ;
;
 ;
;
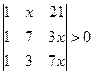
 ;
;
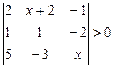 ;
;

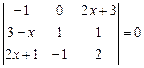 ;
;
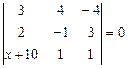 ;
;
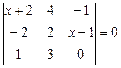
 ;
;
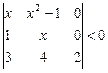
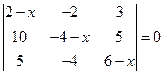
 ;
;

 ;
;


 ;
;

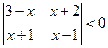
 ;
;