Воспроизводство населения Российской Федерации
Студенты выполняют контрольные работы в соответствии с номером своего варианта, который указывается преподавателем. Номера задач контрольных работ для каждого варианта приведены в таблице 1. Таблица 1
1. Точка совершает гармонические колебания с периодом 6 с и начальной фазой, равной нулю. Определить минимальное время, считая от начала движения, за которое точка сместится от положения равновесия на половину амплитуды. 2. Определить начальную фазу гармонических колебаний материальной точки, если в момент времени, равный нулю, смещение точки от положения равновесия в два раза меньше ее амплитуды колебаний. 3. Точка совершает гармонические колебания, описываемые уравнением х =0,05cos(4π t), где смещение х выражается в метрах, а время t - в секундах. Определить величину ускорения точки через время, равное 0,1 с после начала колебаний. 4. Материальная точка совершает гармонические колебания. Период колебаний равен 0,15 с, максимальная скорость равна 8,0 м/с. Определить амплитуду колебаний. 5. Определить максимальные значения скорости и ускорения материальной точки, совершающей гармонические колебания с амплитудой 3 см и периодом 4 с. 6. Материальная точка совершает гармонические колебания с амплитудой 5,0 см. Максимальное ускорение точки составляет 20 см/с2. Определить циклическую частоту колебаний точки. 7. Максимальная скорость колебаний материальной точки равна 10 см/с, амплитуда колебаний составляет 2,0 см. Определить максимальное ускорение точки. 8. Определить период колебаний материальной точки, совершающей гармонические колебания с амплитудой 15 см, если наибольшая скорость точки равна 30 см/с. 9. Уравнение движения материальной точки дано в виде: х =sin(π t /6), где смещение х выражается в метрах, а время t - в секундах. Через какое минимальное время, считая от начала колебаний, скорость точки достигает максимального значения? 10. Написать уравнение гармонического колебательного движения материальной точки, если ее максимальное ускорение равно 49 см/с2, а период колебаний составляет2,0 с. Смещение точки от положения равновесия в начальный момент времени равно 2,5 см. 11. Материальная точка массой 10 г совершает гармонические колебания по закону х =0,1cos(4π t +π/4), где смещение х выражается в метрах, а время t - в секундах. Найти максимальное значение кинетической энергии этой точки. 12. Материальная точка массой 5,0 г совершает гармонические колебания по закону х =0,2cos(2π t +π/3), где смещение х выражается в метрах, а время t - в секундах. Найти максимальное значение потенциальной энергии этой точки. 13. Шарик, подвешенный к спиральной пружине, совершает вертикальные гармонические колебания с амплитудой 8 см. Определить жесткость пружины, если известно, что максимальная кинетическая энергия шарика составляет 0,8 Дж. 14. Шарик, подвешенный к спиральной пружине, совершает вертикальные гармонические колебания с амплитудой 6 см. Определить полную механическую энергию колебаний шарика, если жесткость пружины составляет 500 Н/м. 15. Частота гармонических колебаний пружинного маятника равна 3,0 с-1. Определить жесткость пружины, если масса маятника равна 0,30 кг. 16. Если увеличить массу груза, подвешенного к спиральной пружине, на 600 г, то период гармонических колебаний груза возрастет в два раза. Определить массу первоначально подвешенного груза. 17. К спиральной пружине подвесили грузик, в результате чего пружина растянулась на 9 см. Каков будет период гармонических колебаний грузика, если пружину с грузиком немного оттянуть вниз и затем отпустить? 18. Однородный диск радиусом 20 см колеблется около горизонтальной оси, проходящей на расстоянии 15 см от центра диска перпендикулярно плоскости диска. Определить период малых колебаний диска относительно этой оси. 19. Тонкий однородный стержень длиной 60 см может свободно вращаться вокруг горизонтальной оси, отстоящей на расстоянии 15 см от его середины. Определить период малых колебаний стержня. 20. Найти отношение длин двух математических маятников, если отношение периодов их колебаний равно 1,50. 21. Определить начальную фазу колебания, получающегося в результате сложения двух одинаково направленных колебаний с одинаковыми периодами и одинаковыми амплитудами. Разность фаз этих колебаний равна π/4. Начальная фаза одного из этих колебаний равна нулю. 22. Найти амплитуду гармонического колебания, полученного от сложения двух одинаково направленных гармонических колебаний, описываемых уравнениями: х 1=0,02sin(5π t +π/2) и х 2=0,03cos(5π t +π/4), где смещения х 1 и х 2 выражаются в метрах, а время t - в секундах. 23. В результате сложения двух одинаково направленных гармонических колебаний с одинаковыми амплитудами и одинаковыми периодами получается результирующее колебание с тем же периодом и той же амплитудой. Найти разность фаз складываемых колебаний. 24. Найти начальную фазу гармонического колебания, получаемого от сложения двух одинаково направленных гармонических колебаний, описываемых уравнениями: х 1=3cos(2π t) и х 2=3cos(2π t +π/4), где смещения х 1 и х 2 выражаются в метрах, а время t - в секундах. 25. Два одинаково направленных гармонических колебания одного периода с амплитудами 10 см и 6,0 см соответственно складываются в одно колебание с амплитудой 14 см. Найти разность фаз складываемых колебаний. 26. Найти амплитуду результирующего колебания, возникающего при сложении двух колебаний одинакового направления и одинаковой частоты и определяемых уравнениями: х 1= А 1sin(ω t) и х 2= А 2sinω(t +τ), где смещения х 1 и х 2 выражаются в метрах, а время t - в секундах. При этом А 1= А 2= 10-2м; ω=π с-1; τ=0,50 с. 27. Материальная точка участвует в двух одинаково направленных гармонических колебаниях, определяемых уравнениями: х 1= А 1sin(ω t) и х 2= А 2cos(ω t), где А 1=1 cм, А 2=2 см. Определить начальную фазу результирующего колебания. 28. Складываются два гармонических колебания одного направления с одинаковыми периодами. Амплитуда каждого колебания равна 2,0 см. Начальные фазы колебаний 29. При сложении двух гармонических колебаний одного направления и одинаковой частоты с амплитудами, равными соответственно 3,0 см и 4,0 см, получается колебание с амплитудой 5,0 см. Найти начальную фазу результирующего колебания, если начальная фаза первого колебания равна нулю. 30. Найти амплитуду результирующего колебания, возникающего при сложении двух гармонических колебаний одинакового направления и одинаковой частоты и определяемых уравнениями: х 1=3sin(ω t) и х 2=4cos(ω t), где смещения х 1 и х 2 выражаются в метрах, а время t - в секундах. 31. Материальная точка участвует в двух взаимно-перпендикулярных колебаниях, определяемых уравнениями: 32. Материальная точка участвует в двух взаимно-перпендикулярных колебаниях одинакового периода с одинаковыми начальными фазами. Амплитуды колебаний соответственно равны 3,0 см и 4,0 см. Найти амплитуду результирующего колебания. 33. Материальная точка участвует в двух взаимно-перпендикулярных колебаниях, определяемых уравнениями: х =2sinω t и у =2cosω t. Определить уравнение траектории точки. 34. Материальная точка участвует в двух взаимно-перпендикулярных колебаниях, определяемых уравнениями: х =cosπ t и у =2cosπ t. Найти уравнение траектории результирующего движения точки. 35. Материальная точка участвует в двух взаимно-перпендикулярных колебаниях, определяемых уравнениями: х =sinπ t и у =2sin(π t +π/2). Найти уравнение траектории движения точки. 36. Материальная точка участвует в двух взаимно-перпендикулярных колебаниях, определяемых уравнениями: х=sinπ t и у=4sin(π t +π). Найти уравнение траектории движения точки. 37. Материальная точка, участвуя в двух взаимно-перпендикулярных колебаниях, движется по окружности. Чему равна разность фаз этих колебаний, если они происходят с одинаковой частотой? 38. Материальная точка одновременно участвует в двух гармонических колебаниях, происходящих по взаимно-перпендикулярным направлениям и описываемых уравнениями: х = А sin2ω t, у = В cos2ω t. Найти траекторию движения точки, приняв величину А равной 2 cм, а величину В равной 3 см. 39. Материальная точка одновременно участвует в двух взаимно- перпендикулярных колебаниях одинаковой частоты и имеющих разность фаз π/2. Амплитуда первого колебания равняется 3 см, а амплитуда второго колебания равняется 4 см. Найти амплитуду результирующего колебания. 40. Материальная точка участвует в двух взаимно-перпендикулярных колебаниях, определяемых уравнениями: х =cos(π t) и у=4cos(π t -π). Найти уравнение траектории движения точки. 41. Амплитуда затухающих колебаний материальной точки за 5 минут уменьшилась в два раза. За какое время, считая от начального момента, амплитуда уменьшится в восемь раз? 42. Найти время релаксации затухающих колебаний материальной точки, если за 5 минут амплитуда ее колебаний уменьшилась в 8 раз. 43. Время релаксации затухающих колебаний материальной точки равно 1 с. В течение какого промежутка времени, считая от начала процесса, амплитуда колебаний уменьшится в 2 раза? 44. Амплитуда затухающих колебаний материальной точки в первой среде уменьшилась в два раза за одну минуту, а при колебаниях этой точки во второй среде такое уменьшение произошло за девять минут. Во сколько раз коэффициент затухания в первой среде больше, чем во второй? 45. Затухающие колебания материальной точки происходят с частотой, равной 1,0 с-1. Логарифмический декремент затухания равен 2,0·10-2. Определить время релаксации. 46. Время релаксации затухающих колебаний материальной точки равно 1,0 с, логарифмический декремент затухания равен 2,0. Определить период колебаний точки. 47. Период затухающих колебаний материальной точки равен 2,0 с. Время релаксации составляет 20 с. Определить логарифмический декремент затухания. 48. Определить, на сколько период затухающих колебаний материальной точки больше периода ее собственных колебаний, равного 1,0 с, если логарифмический декремент затухания равен 0,628. 49. Маленький шарик массой 1,0 г совершает затухающие колебания в вязкой среде с коэффициентом сопротивления 2,0 г/с. За какое время, считая от начала колебаний, амплитуда колебаний шарика уменьшится в 2,0 раза? 50. Число полных колебаний, в течение которых амплитуда затухающих колебаний материальной точки уменьшается в 3,0 раза, равно 100. Определить логарифмический декремент затухания. 51. Циклическая частота, отвечающая резонансу при вынужденных колебаниях материальной точки, равна 1000 с-1. Определить коэффициент затухания, если логарифмический декремент затухания равен 10-3. 52. Затухающие колебания материальной точки происходят с циклической частотой 500,0 с-1. Коэффициент затухания равен 10 с-1. Определить, на сколько собственная циклическая частота колебаний точки больше резонансной. 53. Циклическая частота собственных колебаний материальной точки составляет 500,0 с-1. Определить частоту затухающих колебаний точки, если резонансная циклическая частота равна 499,0 с-1. 54. За 1,2 с амплитуда затухающих колебаний материальной точки уменьшилась в 13 раз. Период затухающих колебаний равен 2,0 с. Определить резонансную циклическую частоту вынужденных колебаний точки. 55. Циклическая частота собственных колебаний материальной точки равна 300 с-1. Циклическая частота, отвечающая резонансу, равна 299 с-1. Определить время релаксации. 56. Колебательная система совершает затухающие колебания с частотой 1000 Гц. Определить частоту собственных колебаний, если резонансная частота равна 998 Гц. 57. Определить логарифмический декремент затухания колебательной системы, для которой резонанс наблюдается при частоте, меньшей собственной частоты, равной 10 кГц, на 2,0 Гц. 58. Период собственных колебаний пружинного маятника равен 0,55 с. В вязкой среде период колебаний того же маятника стал равным 0,56 c. Определить резонансную частоту колебаний. 59. Пружинный маятник (жесткость пружины равна 10 Н/м, масса груза равна 0,10 кг) совершает вынужденные колебания в вязкой среде с коэффициентом сопротивления, равным 2,0·10-2кг/с. Определить резонансную амплитуду, если вынуждающая сила, действующая на маятник, изменяется по гармоническому закону, а ее амплитудное значение равно 10 мН. 60. Маленький шарик совершает вынужденные колебания в среде с коэффициентом сопротивления 1,0 г/с. Считая затухание малым, определить амплитудное значение вынуждающей силы, изменяющейся по гармоническому закону, если резонансная амплитуда равна 50 мм, а частота собственных колебаний шарика равна 10 Гц. 61. Плоская волна длиной 1,7 м распространяется в однородной среде с фазовой скоростью 340 м/с. Найти частоту колебаний материальных точек среды, в которой распространяется волна. 62. Плоская волна распространяется в однородной среде с фазовой скоростью 680 м/с. Найти длину волны, если частота колебании материальных точек среды, в которой распространяется волна, равна 400 Гц. 63. Плоская волна длиной 3,4 м распространяется в однородной среде. Найти фазовую скорость волны, если частота колебаний материальных точек среды, в которой распространяется волна, равна 100 Гц. 64. Плоская волна распространяется в однородной среде. Кратчайшее расстояние между двумя точками среды, колеблющимися в противофазе, равно 1,7 м. Определить фазовую скорость волны, если частота колебаний этих точек равна 50 Гц. 65. Плоская волна распространяется в однородной среде. Кратчайшее расстояние между двумя точками среды, колеблющимися в одинаковой фазе, равно 2 м. Определить частоту колебаний точек, если фазовая скорость волны равна 340 м/с. 66. В однородной среде распространяется плоская волна с частотой 100 Гц и фазовой скоростью 340 м/с. Найти кратчайшее расстояние между двумя точками среды, колебания которых происходят в противофазе. 67. В однородной среде распространяется плоская волна с фазовой скоростью 340 м/с. Найти кратчайшее расстояние между точками среды, разность фаз колебаний которых составляет π/2, если период колебаний точек равен 10-2с. 68. Плоская волна распространяется в однородной среде с частотой 100 Гц с фазовой скоростью 300 м/c. Какое волновое число имеет такая волна? 69. В однородной среде распространяется плоская волна, имеющая волновое число, равное 40π м-1 и фазовую скорость 200 м/с. Определить период колебаний материальных точек среды, в которой распространяется такая волна. 70. В однородной среде распространяется плоская волна. Кратчайшее расстояние между двумя точками среды, колеблющимися в противофазе, равно 1 м. Найти волновое число, соответствующее такой волне. 71. Плоская волна, имеющая частоту 0,5 кГц и амплитуду 0,25 мм, распространяется в упругой однородной среде. Найти максимальную скорость точек среды, в которой распространяется волна. 72. Плоская волна, имеющая амплитуду 2,0 мм, распространяется в однородной среде. Найти частоту колебаний материальных точек среды, в которой распространяется волна, если максимальная скорость, с которой колеблются эти точки, равна 2,0 м/с. 73. Плоская волна, имеющая амплитуду 0,20 м, длину 1,2 м и начальную фазу, равную нулю, распространяется в однородной среде, материальные точки которой осуществляют при этом колебания с периодом 3,0 с. Для точек такой среды, удаленных от источника колебаний на расстояние 2,4 м, найти смещение в момент времени 6,0 с. 74. Плоская волна, имеющая амплитуду 0,30 м, длину 2,8 м и начальную фазу, равную нулю, распространяется в однородной среде, материальные точки которой осуществляют при этом колебания с периодом 2,0 с. Для точек такой среды, удаленных от источника колебаний на расстояние 13,3 м, найти скорость в момент времени 9,0 с. 75. Плоская волна, имеющая амплитуду 0,35 м, длину 1,6 м и начальную фазу, равную нулю, распространяется в однородной среде, материальные точки которой осуществляют колебания с периодом 2,0 с. Для точек такой среды, удаленных от источника колебаний на расстояние 8,0 м, найти ускорение в момент времени 7,0 с. 76. Плоская волна с амплитудой 10 см распространяется в однородной среде. Определить величину смещения точки среды, удаленной от источника колебаний на расстояние, равное 3/4 длины волны, когда от начала колебаний прошло время, равное 0,90 периода колебаний. Начальную фазу колебаний принять равной нулю. 77. Плоская волна с частотой 100 Гц и амплитудой 20 см распространяется в однородной среде. Определить величину скорости точки среды, удаленной от источника колебаний на расстояние, равное 5/6 длины волны, когда от начала колебаний прошло время, равное 0,85 периода колебаний. Начальную фазу колебаний принять равной нулю. 78. Плоская волна с амплитудой 35 мм и частотой 10 Гц распространяется в однородной среде. Определить величину ускорения точки среды, удаленной от источника колебаний на расстояние, равное 2/3 длины волны, когда от начала колебаний прошло время, равное 0,65 периода колебаний. Начальную фазу колебаний принять равной нулю. 79. Плоская волна, имеющая амплитуду 2,0 см и начальную фазу, равную нулю, распространяется с фазовой скоростью 15 м/с в однородной среде, материальные точки которой осуществляют колебания с периодом 1,2 с. Чему равно смещение точки такой среды, находящейся на расстоянии 45 м от источника колебаний в тот момент, когда от начала колебаний источника прошло время, равное 4 с? 80. Две точки однородной среды находятся на расстоянии 50 см друг от друга на прямой, вдоль которой распространяется плоская волна с фазовой скоростью 50 м/с. Период колебаний точек равен 50 мс. Найти разность фаз колебаний в этих точках. 81. На пути световой волны, идущей в воздухе, поставили стеклянную пластинку толщиной 1,0 мм. На сколько изменится при этом оптическая длина пути света, если волна падает на пластинку нормально? 82. На пути световой волны, идущей в воздухе, поставили нормально стеклянную пластинку, при этом оптическая длина пути света, прошедшего через пластинку, увеличилась на 1,0 мм. Определить толщину этой пластинки. 83. На пути световой волны, идущей в воздухе, поставили нормально прозрачную однородную пластинку толщиной 1,0 мм. В результате оптическая длина пути света увеличилась на 1,5 мм. Найти показатель преломления материала пластинки. 84. На тонкую мыльную пленку с показателем преломления 1,33, находящуюся в воздухе, нормально падает монохроматический свет с длиной волны 0,60 мкм. Какова должна быть толщина пленки, если после ее прохождения оптическая длина пути света изменилась на половину длины волны? 85. На тонкую прозрачную пленку толщиной 0,50 мкм, находящуюся в воздухе, нормально падает монохроматический свет с длиной волны 0,70 мкм. Найти показатель преломления пленки, если оптическая разность хода лучей, отраженных от ее верхней и нижней поверхности, составила 1,5 мкм. 86. На тонкую мыльную пленку с показателем преломления 1,33, находящуюся в воздухе, падает нормально пучок белого света. При какой наименьшей толщине пленки отраженный свет с длиной волны 0,55 мкм окажется максимально усиленным в результате интерференции? 87. На тонкую однородную прозрачную пленку, находящуюся в воздухе, нормально падает монохроматический свет с длиной волны 600 нм. Найти показатель преломления пленки, если минимальная толщина пленки, при которой наблюдается максимальное усиление света при наблюдении интерференции в отраженном свете, составляет 100 нм. 88. На мыльную пленку с показателем преломления 1,33, находящуюся в воздухе, нормально падает монохроматический свет с длиной волны 600 нм. Определить минимальную толщину пленки, при которой отраженный от нее свет окажется максимально ослабленным в результате интерференции. 89. На тонкую стеклянную пластинку, находящуюся в воде, нормально падает свет с длиной волны 600 нм. Определить минимальную толщину пластинки, при которой отраженный от нее свет окажется максимально ослабленным в результате интерференции. 90. Монохроматическая волна длиной 600 нм падает под углом 30° на находящуюся в воздухе мыльную пленку с показателем преломления 1,33. При какой наименьшей толщине пленки отраженные световые лучи будут максимально ослаблены при интерференции? 91. На тонкую стеклянную пластинку, находящуюся в воде, нормально падает свет с длиной волны 600 нм. Определить минимальную толщину пластинки, при которой отраженный от нее свет окажется максимально усиленным в результате интерференции. 92. На мыльную пленку с показателем преломления 1,33 падает белый свет под углом 45°. При какой наименьшей толщине пленки отраженные лучи желтого цвета с длиной волны 600 нм будут максимально усилены? Пленка находится в воздухе. 93. Плосковыпуклая линза выпуклой стороной лежит на стеклянной пластинке и освещается монохроматическим светом, падающим на линзу нормально. При этом радиусы двух соседних темных колец Ньютона в отраженном свете равны соответственно 4,0 мм и 4,9 мм. Найти порядковые номера колец, если наблюдение проводится в воздухе. 94. Расстояние между пятым и двадцать пятым светлыми кольцами Ньютона равно 11 мм, радиус кривизны плосковыпуклой линзы равен 3,0 м. Найти длину волны монохроматического света, падающего нормально на линзу. Наблюдение проводится в воздухе в отраженном свете. 95. Расстояние между 16 и 9 темными кольцами Ньютона при наблюдении интерференции света с длиной волны 625 нм в воздухе в отраженном свете составляет 2,50 мм. Определить радиус кривизны плосковыпуклой линзы, на которую свет падает нормально. 96. Найти расстояние между третьим и шестнадцатым темными кольцами Ньютона, если расстояние между вторым и двадцатым темными кольцами равно 4,8 мм. Наблюдение проводится в воздухе в отраженном свете. Свет падает на плосковыпуклую линзу нормально. 97. Между стеклянной пластинкой и лежащей на ней стеклянной плосковыпуклой линзой налита жидкость, показатель преломления которой меньше показателя преломления стекла. Радиус восьмого темного кольца Ньютона при наблюдении интерференции в отраженном свете равен 2,0 мм. Радиус кривизны выпуклой поверхности линзы равен 1 м. Найти показатель преломления жидкости при нормальном падении света с длиной волны 700 нм на линзу. 98. Плосковыпуклая линза выпуклой стороной лежит на стеклянной пластинке. Определить толщину слоя воздуха там, где в отраженном свете с длиной волны 0,60 мкм видно первое светлое кольцо Ньютона. Свет падает на линзу нормально. 99. Плосковыпуклая линза выпуклой стороной лежит на стеклянной пластинке. Определить толщину слоя воздуха там, где в отраженном свете с длиной волны 0,750 мкм видно первое темное кольцо Ньютона. Свет падает на линзу нормально. 100. Установка для наблюдения колец Ньютона в отраженном свете освещается монохроматическим светом, падающим нормально на плоско-выпуклую линзу. Первоначально измерения провели в воздухе, а затем пространство между линзой и стеклянной пластинкой заполнили жидкостью, в результате чего радиусы темных колец уменьшились в 1,25 раза. Найти показатель преломления жидкости. 101. Определить постоянную дифракционной решетки, если при ее освещении светом с длиной волны 650 нм второй дифракционный максимум виден под углом 15°. Свет падает на решетку нормально. 102. Под каким углом виден максимум второго порядка при наблюдении дифракции света длиной волны 700 нм, падающим нормально на дифракционную решетку с периодом 700 мкм? 103. Сколько штрихов на каждый сантиметр длины имеет дифракционная решетка, если четвертый дифракционный максимум, даваемый решеткой при нормальном падении на нее света длиной волны 600 нм, отклонен от нормали на угол 6,00°? 104. Дифракционная решетка, имеющая 500 штрихов на каждый миллиметр длины, освещается светом, падающим нормально. Второй дифракционный максимум виден под углом 30°. Определите длину волны света, падающего на решетку. 105. Дифракционная решетка освещена нормально падающим монохроматическим светом. При этом дифракционный максимум второго порядка наблюдается под углом 14°. Под каким углом наблюдается максимум третьего порядка? 106. Дифракционная решетка с периодом 100 мкм освещается светом с длиной волны 500 нм, падающим нормально. Определить угол между направлениями на первые дифракционные максимумы такой решетки, симметрично расположенные относительно центрального дифракционного максимума. 107. Дифракционная решетка содержит 200 штрихов на каждый миллиметр длины. На решетку нормально падает монохроматический свет с длиной волны 600 нм. Максимум, какого наибольшего порядка дает эта решетка? 108. Дифракционная решетка, имеющая 200 штрихов на каждый миллиметр длины, освещается монохроматическим светом длиной волны 500 нм, падающим на решетку нормально. Сколько максимумов дает эта решетка? 109. Дифракционная решетка, имеющая период 800 нм, освещается светом, падающим нормально. Найти длину волны света, падающего на решетку, если максимальное число дифракционных максимумов, наблюдаемых с помощью этой решетки, равно 5. 110. Постоянная дифракционной решетки в 4 раза больше длины световой волны монохроматического света, нормально падающего на ее поверхность. Определить угол между двумя первыми дифракционными минимумами, симметрично расположенными относительно центрального дифракционного максимума. 111. Угол между первыми дифракционными максимумами, расположенными симметрично относительно центрального максимума, образующимися при освещении дифракционной решетки монохроматическим светом, падающим на решетку нормально, равен 10°. Определить, во сколько раз период такой решетки больше длины волны падающего на нее света. 112. При освещении дифракционной решетки белым светом спектры второго и третьего порядка частично перекрывают друг друга. На какую длину волны в спектре второго порядка накладывается волна длиной 400 нм, соответствующая фиолетовой границе в спектре третьего порядка? 113. Чему равна постоянная дифракционной решетки, если эта решетка может разрешить в первом порядке линии спектра калия с длинами волн соответственно 404,4 нм и 404,7 нм? Ширина решетки равна 3,0 см. 114. В спектре какого порядка могут быть разрешены две спектральные линии с длинами волн соответственно 500,0 нм и 500,1 нм, если период дифракционной решетки равен 10 мкм, а ее длина равняется 2,50 см? 115. Найти длину дифракционной решетки, если в спектре второго порядка такая решетка может разрешить две спектральные линии с длинами волн соответственно 600,0 нм и 600,1 нм. Период решетки равен 5,00 мкм. 116. Период одной дифракционной решетки равен 10 мкм, а период другой решетки равен 5,0 мкм. Найти отношение угловых дисперсий этих решеток в спектре первого порядка. 117. Определить угловую дисперсию дифракционной решетки для света длиной волны 589,0 нм в спектре первого порядка. Постоянная решетки равна 2,5 мкм. 118. Для какой длины волны дифракционная решетка с постоянной 5,0 мкм имеет угловую дисперсию, равную 6,3·105 рад/м в спектре третьего порядка? 119. Угловая дисперсия дифракционной решетки в спектре второго порядка для длины волны 500 нм равна 4,08·105 рад/м. Определить постоянную дифракционной решетки. 120. Определить линейную дисперсию дифракционной решетки для света длиной волны 600 нм в спектре первого порядка. Постоянная решетки равна 3,00 мкм. Фокусное расстояние линзы, проектирующей спектр на экран, равно 50 см. Ответ выразить в миллиметрах на нанометр. 121. Определить угол падения, при котором наблюдается полная поляризация при отражении света от стекла, находящегося в воздухе. 122. При отражении света от плоской поверхности некоторого материала, находящегося в воздухе, полная поляризация света наблюдается при угле падения 56,3°. Определить показатель преломления материала. 123. Под каким углом к горизонту должно находиться Солнце, чтобы его лучи, отраженные от горизонтальной водной поверхности, были полностью поляризованы? 124. Пучок естественного света, идущий в воде, отражается от грани алмаза, погруженного в воду. При каком угле падения света на поверхность алмаза отраженный луч окажется полностью поляризованным? 125. Пучок естественного света, идущий в жидкости, отражается от горизонтально расположенной стеклянной пластинки, погруженной в жидкость. Найти показатель преломления жидкости, если отраженный свет при падении света на поверхность пластинки под углом 48,4° оказывается полностью поляризованным. 126. Угол Брюстера при падении света из воздуха на кристалл каменной соли равен 57°. Определить скорость света в этом кристалле. 127. Скорость света в стекле составляет 2,0·108 м/с. Определить для стекла угол Брюстера. 128. Пучок естественного света, идущий в воде, отражается от грани прозрачного кристалла, погруженного в воду. Определить показатель преломления кристалла, если при угле падения света 62° отраженный луч оказывается полностью поляризованным. 129. Степень поляризации частично поляризованного света равна 0,75. Определить отношение максимальной интенсивности света, пропускаемого поляризатором, к минимальной. 130. В частично-поляризованном свете амплитуда колебаний светового вектора, соответствующая максимальной интенсивности света, в 2 раза больше амплитуды колебаний, соответствующей минимальной интенсивности. Определить степень поляризации света. 131. Анализатор в 2,0 раза уменьшает интенсивность плоскополяризованного света, приходящего к нему от поляризатора. Определить угол между плоскостями пропускания поляризатора и анализатора. Поглощением света пренебречь. 132. Угол между плоскостями пропускания поляризатора и анализатора увеличился с 30° до 45°. Определить, во сколько раз изменилась при этом интенсивность прошедшего через них плоскополяризованного света. Поглощением света в поляризаторе и анализаторе пренебречь. 133. Определить плотность чистой оптически активной жидкости, содержащейся в стеклянной трубке длиной 8,0 см, если при прохождении трубки плоскость поляризации света поворачивается на угол 137°. Удельное вращение жидкости равно 1,69 град·м3/(м·кг). 134. Раствор глюкозы концентрацией 0,28 г/см3, налитый в стеклянную трубку длиной 15 см, поворачивает плоскость поляризации монохроматического света, проходящего через этот раствор, на угол, равный 32°. Определить удельное вращение раствора глюкозы. 135. При прохождении через трубку длиной 20 см с сахарным раствором плоскость поляризации света поворачивается на угол, равный 5,0°. Удельное вращение раствора сахара равно 0,60 град/(м·%). Определить концентрацию раствора. 136. При прохождении света через слой 10 % раствора сахарозы толщиной 15 см плоскость поляризации повернулась на угол, равный 12,9°. В другом растворе сахарозы толщиной 12 см плоскость поляризации повернулась на угол, равный 7,2°. Найти концентрацию сахарозы во втором растворе. 137. При прохождении света через слой 5% раствора сахара толщиной 10 см плоскость поляризации света поворачивается на угол, равный 5°. На сколько градусов повернется плоскость поляризации этого света при прохождении 10% раствора сахара толщиной 20 см? 138. Концентрация сахара в первой трубке меньше, чем во второй, в два раза, а длина первой трубки больше, чем второй в 3 раза. Во сколько раз угол поворота плоскости поляризации при прохождении света через первую трубку больше, чем через вторую? 139. При пропускании плоскополяризованного света через растворы сахарозы угол поворота плоскости поляризации в первом растворе меньше, чем во втором, в 4 раза, а толщина слоя первого раствора больше, чем второго, в 5 раз. Во сколько раз концентрация сахарозы в первом растворе меньше, чем во втором? 140. Угол поворота плоскости поляризации света в первом растворе сахарозы меньше, чем во втором, в три раза, а концентрация сахарозы в первом растворе меньше, чем во втором, в 6 раз. Во сколько раз толщина слоя сахарозы в первом растворе больше, чем во втором? ОТВЕТЫ 1. t =1с 2.
|

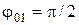 и
и  . Определить амплитуду результирующего колебания.
. Определить амплитуду результирующего колебания. и
и 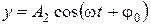 . Определить уравнение траектории точки, если амплитуда первого колебания равна 5,0 см, а второго колебания равна 10 см.
. Определить уравнение траектории точки, если амплитуда первого колебания равна 5,0 см, а второго колебания равна 10 см. 3. а =2,4м/с2 4. А =0,19м 5. υ max =4,7cм/c; а max=7,4см/с2 6.
3. а =2,4м/с2 4. А =0,19м 5. υ max =4,7cм/c; а max=7,4см/с2 6.  =2,0с-1 7. а max=50cм/с2 8. Т =3,1с 9. t min=6,0с 10. х =5,0cos(π t +π/3), см 11. Т max=8мДж 12. Е n max=4мДж 13. k =250 Н/м 14. Е =0,9Дж 15. k =0,11 кН/м 16. m =200г 17. Т =0,6с 18. Т =1,1с 19. Т =1,2с 20. (
=2,0с-1 7. а max=50cм/с2 8. Т =3,1с 9. t min=6,0с 10. х =5,0cos(π t +π/3), см 11. Т max=8мДж 12. Е n max=4мДж 13. k =250 Н/м 14. Е =0,9Дж 15. k =0,11 кН/м 16. m =200г 17. Т =0,6с 18. Т =1,1с 19. Т =1,2с 20. (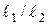 )=2,25 21.
)=2,25 21.  22. А =4,6 см 23. Δφ=120° 24. φ0=π/4 25. Δφ= π/3 26. А =1,4∙10-2м 27. φ0=63° 28. А =3,9 см 29. φ0=53° 30. А =5м 31. y =2 x 32. А =5,0см 33. x 2+ y 2=4 34. y =2 x 35. x 2+ y 2/4=1 36. y =-4 x 37. Δφ= π/2 38. х 2/4+ y 2/9=1 39. А =5см 40. y =-4 x 41. Δ t =15мин 42. τ=2,4мин 43. Δ t =0,7с 44. в 9 раз 45. τ=50с 46. Т =2,0с 47. Ө=0,10 48. на 5,0мс 49. Δ t =0,69с 50. Ө =1,1∙10-2 51. β=1с-1 52. больше на 0,20Гц 53. ω=499,5с-1 54. ωр=2,3с-1 55. τ=5,8·10-2с 56. ν0=1002Гц 57. Ө=8,9 ∙10-2 58. νр=1,8Гц 59. А р=5,0см 60. F 0=3,1мН 61. ν=200с-1 62. λ=1,7м 63. υ=340м/с 64. υ=170м/с 65. ν=170с-1 66. ℓ;=1,7м 67. ℓ;=0,85м 68. k =2,1м-1 69. Т =2,5∙10-4с 70. k =π м-1 71. υmax=0,79м/с 72. ν=0,16Гц 73. ξ=0,20м 74.
22. А =4,6 см 23. Δφ=120° 24. φ0=π/4 25. Δφ= π/3 26. А =1,4∙10-2м 27. φ0=63° 28. А =3,9 см 29. φ0=53° 30. А =5м 31. y =2 x 32. А =5,0см 33. x 2+ y 2=4 34. y =2 x 35. x 2+ y 2/4=1 36. y =-4 x 37. Δφ= π/2 38. х 2/4+ y 2/9=1 39. А =5см 40. y =-4 x 41. Δ t =15мин 42. τ=2,4мин 43. Δ t =0,7с 44. в 9 раз 45. τ=50с 46. Т =2,0с 47. Ө=0,10 48. на 5,0мс 49. Δ t =0,69с 50. Ө =1,1∙10-2 51. β=1с-1 52. больше на 0,20Гц 53. ω=499,5с-1 54. ωр=2,3с-1 55. τ=5,8·10-2с 56. ν0=1002Гц 57. Ө=8,9 ∙10-2 58. νр=1,8Гц 59. А р=5,0см 60. F 0=3,1мН 61. ν=200с-1 62. λ=1,7м 63. υ=340м/с 64. υ=170м/с 65. ν=170с-1 66. ℓ;=1,7м 67. ℓ;=0,85м 68. k =2,1м-1 69. Т =2,5∙10-4с 70. k =π м-1 71. υmax=0,79м/с 72. ν=0,16Гц 73. ξ=0,20м 74. 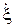 =0,94 м/с 75.
=0,94 м/с 75.  =3,5м/с2 76.
=3,5м/с2 76.  =5,9см 77.
=5,9см 77. 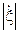 =13м/с 78.
=13м/с 78. 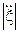 =14 м/с2 79.
=14 м/с2 79. 


