Решение задачи математического программирования

 

 

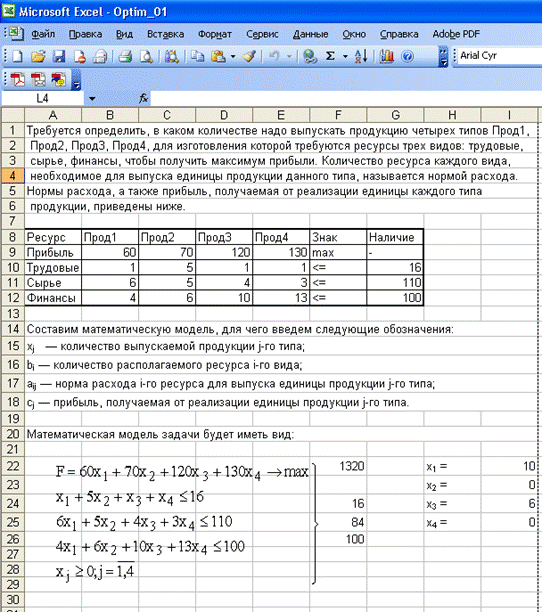
Рассмотрим информационную технологию решения задачи математического программирования на примере задачи линейного программирования на следующем примере.

Требуется определить, в каком количестве надо выпускать продукцию четырех типов Прод1, Прод2, Прод3, Прод4, для изготовления которой требуются ресурсы трех видов: трудовые, сырье, финансы, чтобы получить максимум прибыли. Количество ресурса каждого вида, необходимое для выпуска единицы продукции данного типа, называется нормой расхода. Нормы расхода, а также прибыль, получаемая от реализации единицы каждого типа продукции, приведены ниже в табл. 5.

Таблица № 3.5

Исходные данные задачи линейного программирования

Ресурс	Прод1	Прод2	Прод3	Прод4	Знак	Наличие
Прибыль					max	-
Трудовые					<=
Сырье					<=
Финансы					<=

 

Составим математическую модель, для чего введем следующие обозначения:

х_j – количество выпускаемой продукции j -го типа;

b_i – количество располагаемого ресурса i -го вида;

a_ij – норма расхода i -го ресурса для выпуска единицы продукции j -го типа;

c_j – прибыль, получаемая от реализации единицы продукции j -го типа;

n – количество типов выпускаемой продукции;

m – количество ограничений на ресурсы.

Тогда задача линейного программирования в общем виде может быть записана.

Задача сводится к нахождению такого вектора X, при котором целевая функция F (X) принимает максимальное (или минимальное) значение с учетом ограничений, задаваемых нестрогими линейными неравенствами (или линейными уравнениями). В задачах линейного программирования целевая функция F (X) тоже должна быть линейной.

Для приведенных выше конкретных данных задача линейного программирования записывается в виде:

В ячейках A 8: G 12 листа 2 MS (см. рис. 5) Exсel разместим таблицу исходных данных задачи (см. табл. 3.5). Ячейки I 22: I 25 выделим для формирования вектора решения задачи . В ячейке F 22 запишем выражение для вычисления правой части целевой функции. В ячейках F 24: F 26 сформируем формулы для вычисления левых частей ограничений (в виде нестрогих неравенств). Формулы, записанные в ячейки F 22, F 24: F 26 приведены в табл. 3.6.

Таблица 3.6

Формулы целевой функции и ограничений

№ п/п	Ячейка	Формула
1.	F 22	= I 22* B 9+ I 23* C 9+ I 24* D 9+ I 25* E 9
2.	F 24	= I 22* B 10+ I 23* C 10+ I 24* D 10+ I 25* E 10
3.	F 25	= I 22* B 11+ I 23* C 11+ I 24* D 11+ I 25* E 11
4.	F 26	= I 22* B 12+ I 23* C 12+ I 24* D 12+ I 25* E 12

 

Для решения задачи линейного программирования необходимо в пункте главного меню MS Excel “С е рвис” выбрать подпункт “Поиск р ешения…”. Если в пункте главного меню MS Excel “С е рвис” отсутствует подпункт “Поиск р ешения…”, то необходимо в пункте главного меню “С е рвис” выбрать подпункт “Надстро й ки” и в окне “Надстройки” поставить галочку в строке “Поиск решения…”. Если же в окне “Надстройки” отсутствует строка “Поиск решения…”, то следует переустановить MS Excel.

Рис. 3.5 Задача линейного программирования

Вид окна “Надстройки” представлен на рис. 3.6.

Рис. 3.6. Окно “Надстройки”

На рис. 3.7 представлено окно “Поиск решения”

Рис. 3.7. Окно “Поиск решения”

В окне “Поиск решения” необходимо установить целевую ячейку $ F $22 (F 22) равной максимальному значению (по условию задачи). В поле ниже метки с заголовком “Измен я я ячейки:” необходимо отметить ячейки вектора решения задачи линейного программирования. Ниже метки с заголовком “Ограничения:” с помощью кнопки “Добавить” следует сформировать ограничения задачи линейного программирования. Выделение ячеек и формирование ограничений реализуется в режиме конструктора (адреса ячеек в выражения вставляются на основе технологии визуального программирования).

При нажатии кнопки “Выполнить” в ячейках I 22: I 25 формируется вектор решения задачи линейного программирования (см. рис. 3.8). Кроме этого в ячейке F 22 формируется значение целевой функции при найденном векторе решения. А в ячейках F 24: F 26 вычисляются значения левых частей ограничений при найденном векторе решения задачи линейного программирования.

Рис. 3.8. Решение задачи линейного программирования