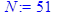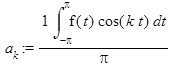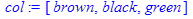Постановка задачи
Написать программу на языке программирования (Бейсик, Паскаль) для решения следующей задачи (10 вариантов задания). Построить блок-схемы задачи и вспомогательных частей алгоритма. Оформление графиков и таблиц выполнять средствами математических и инженерных пакетов.
Задача: Рассматривается функция F(t), представляющая собой периодический (период 2π) сигнал единичной амплитуды длительности T. Значение величины T есть наименьший положительный корень полинома (таблица 1- по вариантам), который вычисляется любым из известных методов нахождения корней уравнений. 1. Программу, реализующую вычисление корня Т, написать на языке программирования Pascal ABC. Для построенного сигнала вычислить по формулам Бесселя коэффициенты конечной суммы Фурье и записать их в файл. 2. С помощью языка программирования математического пакета Maple вычислить для аналогового сигнала своего варианта коэффициенты конечной суммы Фурье (аппроксимирующего тригонометрического полинома) в аналитической форме, построить графики исходного сигнала, тригонометрического полинома для нескольких степеней, а также графики спектров амплитуд дискретного (с коэффициентами из файла, вычисленными на Паскале) и аналогового сигнала.
Структура отчета
1. Формат А4. 2. Титул 3. Постановка задачи 4. Алгоритмы решения вспомогательных задач 5. Блок-схемы 6. Общая структура программы на языке программирования 7. Результаты расчетов, графики 8. Литература
Варианты заданий
Таблица 1. Варианты полиномов (номер варианта определяется по последней цифре студенческого билета)
Текст программы на Pascal
unit Pomogaev_Krasheninnikov;
interface
uses Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms, Dialogs, StdCtrls;
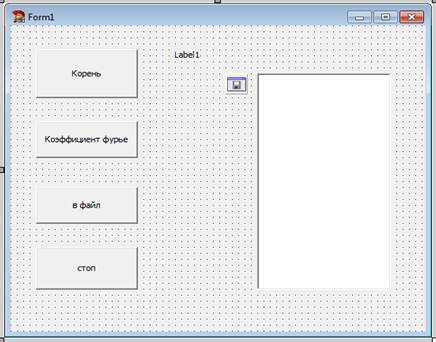
type TForm1 = class(TForm) Label1: TLabel; ListBox1: TListBox; Button1: TButton; Button2: TButton; Button3: TButton; Button4: TButton; SaveDialog1: TSaveDialog; procedure Button4Click(Sender: TObject); procedure Button1Click(Sender: TObject); procedure Button3Click(Sender: TObject); procedure Button2Click(Sender: TObject); private { Private declarations } public { Public declarations } end;
var Form1: TForm1;
implementation
{$R *.dfm}//===================================================== const eps=0.001; x0=4; n=32; m=50; h=2*pi/n; var T:real; fn:string; ft:text; a,b:array[0..m]of real;
function polynom(x:real):real; begin polynom:=x*x*x*x*x-7*x-14; end;
function deriv(x:real):real; begin deriv:=5*sqr(sqr(x))-7; end;
procedure Koren(x0,eps:real;var root:real); var x:real; begin repeat x:=x0-polynom(x0)/deriv(x0); x0:=x; until abs(polynom(x))<eps; root:=x; end;
procedure ZAPIS; var k:integer; begin for k:= 0 to m do writeln (ft,k:3,a[k]:12:3,b[k]:16:4); Closefile(ft); end;
function signal(x:real):real; begin signal:=0; if x <T then signal:=1; end;
//========================================================== procedure Fourier; var k,j:integer; x,h,p,q:real; s1,s2,s3:string; begin h:=2*pi/n; for k:= 0 to m do begin p:=0; q:=0; for j:= 0 to n do begin x:=j*h; p:=p+signal(x)*cos(k*x); q:=q+signal(x)*sin(k*x); end; a[k]:=2/N*p; b[k]:=2/N*q; str(k:4,s1); str(a[k]:10:3,s2); str(b[k]:8:4,s3); Form1.ListBox1.Items.Add(s1+s2+s3); end; end;
/========================================================== procedure TForm1.Button1Click(Sender: TObject); begin Koren(x0,eps,T); Label1.Caption:='Корень='+floattostr(T); end;
procedure TForm1.Button2Click(Sender: TObject); begin Label1.Caption:='Коэффициент фурье'; Fourier end;
procedure TForm1.Button3Click(Sender: TObject); begin if SaveDialog1.Execute then begin fn:=SaveDialog1.FileName; Label1.Caption:='Pomogaev_Krasheninikov'+fn; Assignfile(ft,fn);rewrite(ft); ZAPIS; end; end;
procedure TForm1.Button4Click(Sender: TObject); begin close; end; end.
Результаты вычислений
0 0.625 0.0000 1 0.336 0.4098 2 -0.058 0.2903 3 -0.037 0.0198 4 0.107 0.0442 5 0.038 0.1244 6 -0.024 0.0358 7 0.054 -0.0054 8 0.063 0.0625 9 -0.004 0.0447 10 0.024 -0.0160 11 0.067 0.0202 12 0.018 0.0442 13 0.006 -0.0112 14 0.058 -0.0115 15 0.040 0.0331 16 0.000 0.0000 17 0.040 -0.0331 18 0.058 0.0115 19 0.006 0.0112 20 0.018 -0.0442 21 0.067 -0.0202 22 0.024 0.0160 23 -0.004 -0.0447 24 0.062 -0.0625 25 0.054 0.0054 26 -0.024 -0.0358 27 0.038 -0.1244 28 0.107 -0.0442 29 -0.037 -0.0198 30 -0.058 -0.2903 31 0.336 -0.4098 32 0.625 -0.0000 33 0.336 0.4098 34 -0.058 0.2903 35 -0.037 0.0198 36 0.107 0.0442 37 0.038 0.1244 38 -0.024 0.0358 39 0.054 -0.0054 40 0.063 0.0625 41 -0.004 0.0447 42 0.024 -0.0160 43 0.067 0.0202 44 0.018 0.0442 45 0.006 -0.0112 46 0.058 -0.0115 47 0.040 0.0331 48 0.000 0.0000 49 0.040 -0.0331 50 0.058 0.0115
Форма
Работающая программа
Решение задачи средствами Maple Программа построения АЧХ для периодической функции, заданной аналитически на периоде
> restart;with(plots):;with(plottools):; > N:=51;
> P:=x^5-7*x-14; #полином
> T:=fsolve(P,x=0..3);
N - число гармоник > plot(P,x=T-0.5..T+0.5,thickness=2,color=blue);
> f:=proc(t) local z; z:=piecewise(t<0,0,t<T,1,0);end: > plot(f(x),x=-1..2*Pi,color=blue,thickness=2,discont=true);
> Коэффициенты ряда Фурье вычисляются в аналитической форме (если функция F(t) допускает вычисление первообразной) по формулам
Интегрирование выполняется по любому отрезку длины периода > > a0:=1/Pi*Int(f(t),t=-Pi..Pi):value(%);
> > ak:=1/Pi*Int(f(t)*cos(k*t),t=-Pi..Pi):value(%);
> bk:=1/Pi*Int(f(t)*sin(k*t),t=-Pi..Pi):;value(%);
> A:=seq(evalf(subs(k=n,ak),5),n=1..N);
> B:=seq(evalf(subs(k=n,bk),5),n=1..N);
> Аппроксимация функции конечной суммой ряда Фурье есть тригонометрический полином степени n. > Trig:=proc(t,n) local z,k;global a0,A,B; z:=a0/2+sum(A[k]*cos(k*t)+B[k]*sin(k*t),k=1..n); end;
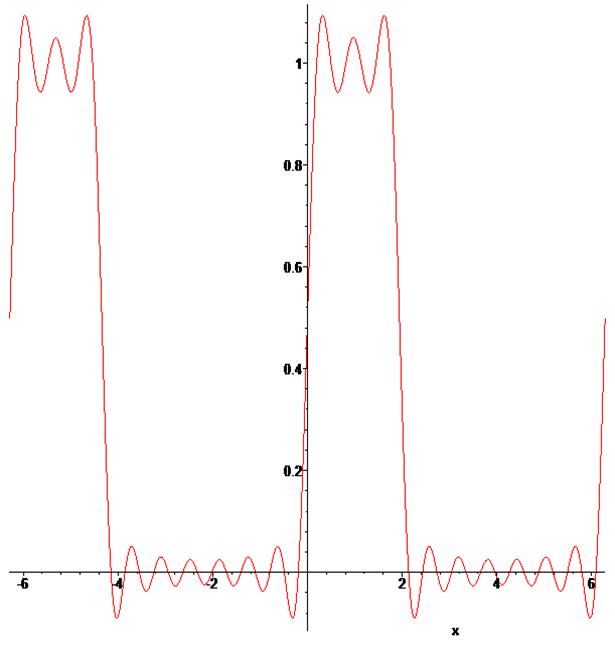
> > > > > plot(Trig(x,10),x=-2*Pi..2*Pi,numpoints=1000);
> > > > Совместный график > ris1:=plot(Trig(x,20),x=-2*Pi..2*Pi,numpoints=1000): > ris2:=plot(f(x),x=-Pi..Pi,thickness=3,color=blue): > display(ris1,ris2);
> col:=[brown,black,green];
> Ris:=seq(plot(Trig(x,3*n),x=-2*Pi..2*Pi,numpoints=100,color=col[n]),n=1..3): > display(Ris,ris2);
> > График спектра амплитуд > k:='k';c:=array(0..N);num:=array(0..N);
> c[0]:=evalf(abs(a0),3); num[0]:=0;
> for k from 1 to N do c[k]:=evalf(abs(A[k]+I*B[k]),3): num[k]:=k; #print(k,num[k],c[k]); end:; > > Risc:=zip((x,y)->[x,y],num,c): > arr:=array(0..N);
> for i from 0 to N do arr[i]:=arrow([i,0],[i,c[i]],0.2,0.2,0,color=black); end:; > Ar:=convert(arr,list):; > Rsym:=plot(Risc,style=point,symbol=circle,symbolsize=20,color=blue,title=`спектр амплитуд`): > display(Ar,Rsym);
Чтение коэффициентов Фурье, вычисленных программой на Паскале
> fn:=`d:\\Koeff`;
> L:=readdata(fn,3):; > with(linalg): > Nkoef:=vectdim(L);
> j:='j';
> for j from 1 to Nkoef do c[j-1]:=evalf(sqrt(L[j,2]^2+L[j,3]^2),4); #print(j,c[j-1]); end: > for i from 0 to Nkoef do arr[i]:=arrow([i,0],[i,c[i]],0.2,0.2,0,color=blue); end:; > Ardiskr:=convert(arr,list):; > Rlin:=plot(Risc,thickness=2,color=brown,title=`сравнение спектров амплитуд`): > display(Ardiskr,Rlin,Ar,Rsym);
> > > >
|