Таблица Бинарные отношения, которые используются в принципах выбора
| №
| Принцип выбора
| Бинарное отношение
|
|
| Парето
| 
|
|
| Слейтер
| 
|
|
| Джофриона
| 
|
|
| По эталону
| 
|
|
| Свертка критериев
| 
|
|
| Лексикографический
| 
|
|
| Последовательных уступок
| 

|
Бинарные отношения, которые определяются лишь знаками разности состовляющих значений векторов критериев  и
и  для каждой пары альтернатив a и b соответственно, называется координатным, то есть
для каждой пары альтернатив a и b соответственно, называется координатным, то есть  , где А – носитель отношения Р,
, где А – носитель отношения Р,  - вектор знаков разности соответствующих компонент векторов критериев,
- вектор знаков разности соответствующих компонент векторов критериев,
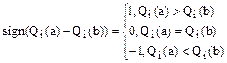
F – логическая функция равная 1, когда aPb, и 0, когда a  b.
b.
Бинарные отношения, которые определяются лишь значениями модулей разности векторов 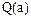 и
и  альтернатив a и b соответственно, называется модульным, то есть
альтернатив a и b соответственно, называется модульным, то есть  , где
, где  - вектор модулей разности соответствующих компонент критериев, Ф – логическая функция равная 1, когда aPb, и 0, когда a
- вектор модулей разности соответствующих компонент критериев, Ф – логическая функция равная 1, когда aPb, и 0, когда a  b.
b.
Бинарные отношения, которые определяются знаками и модулями разности одноименных состовляющих вектора критериев, называется координатно-модульным, то есть  .
.
Следует помнить, что тождественные механизмы выбора могут быть формально представлены несколькими способами. Так выбор по принципам Парето может рассматриваться как агрегация отношений, каждое из которых порождено соответствующей составляющей вектора критериев. Кроме того, всегда можно вместо мажорант искать максимумы двойственных отношений вследствие того, что справедливо соотношение  .
.
Чтобы обеспечить поиск максимумов, отношение считается обычно рефлексивным, то есть существующее отношение Q дополняется до рефлексивного  , где Е – диагональное отношение. Когда определяются мажоранты, отношение считается антирефлексивным, P=Q\E. Если необходимо осуществить выбор недоминирующих альтернатив в квазипорядке, целесообразно его факторизировать по симметричной составляющей (полученное фактор-отношение будет отношением порядка), привести к антирефлексивному виду и выбрать мажоранты приведенного отношения. Каждая из мажорант таким образом может включать в себя одну или несколько эквивалентных по качеству альтернатив первичного отношения, из числа которых и осуществляется окончательный выбор.
, где Е – диагональное отношение. Когда определяются мажоранты, отношение считается антирефлексивным, P=Q\E. Если необходимо осуществить выбор недоминирующих альтернатив в квазипорядке, целесообразно его факторизировать по симметричной составляющей (полученное фактор-отношение будет отношением порядка), привести к антирефлексивному виду и выбрать мажоранты приведенного отношения. Каждая из мажорант таким образом может включать в себя одну или несколько эквивалентных по качеству альтернатив первичного отношения, из числа которых и осуществляется окончательный выбор.








 и
и  для каждой пары альтернатив a и b соответственно, называется координатным, то есть
для каждой пары альтернатив a и b соответственно, называется координатным, то есть  , где А – носитель отношения Р,
, где А – носитель отношения Р,  - вектор знаков разности соответствующих компонент векторов критериев,
- вектор знаков разности соответствующих компонент векторов критериев,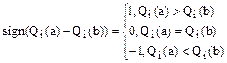
 b.
b.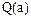 и
и  альтернатив a и b соответственно, называется модульным, то есть
альтернатив a и b соответственно, называется модульным, то есть  , где
, где  - вектор модулей разности соответствующих компонент критериев, Ф – логическая функция равная 1, когда aPb, и 0, когда a
- вектор модулей разности соответствующих компонент критериев, Ф – логическая функция равная 1, когда aPb, и 0, когда a  .
. .
. , где Е – диагональное отношение. Когда определяются мажоранты, отношение считается антирефлексивным, P=Q\E. Если необходимо осуществить выбор недоминирующих альтернатив в квазипорядке, целесообразно его факторизировать по симметричной составляющей (полученное фактор-отношение будет отношением порядка), привести к антирефлексивному виду и выбрать мажоранты приведенного отношения. Каждая из мажорант таким образом может включать в себя одну или несколько эквивалентных по качеству альтернатив первичного отношения, из числа которых и осуществляется окончательный выбор.
, где Е – диагональное отношение. Когда определяются мажоранты, отношение считается антирефлексивным, P=Q\E. Если необходимо осуществить выбор недоминирующих альтернатив в квазипорядке, целесообразно его факторизировать по симметричной составляющей (полученное фактор-отношение будет отношением порядка), привести к антирефлексивному виду и выбрать мажоранты приведенного отношения. Каждая из мажорант таким образом может включать в себя одну или несколько эквивалентных по качеству альтернатив первичного отношения, из числа которых и осуществляется окончательный выбор.


