Теория подобия как основа моделирования потоков
При изучении явлений, происходящих в машинах и сооружениях, наука широко пользуется методом моделирования этих явлений в лабораторных условиях. Преимущество такого метода заключается в том, что изучение физических явлений может быть произведено на модели значительно проще, полнее и выгоднее, чем в натуре. Однако результаты опытов с моделью могут быть использованы для решения задач только в том случае, если при проведении опытов соблюдаются определенные законы моделирования – законы подобия. Нахождение критериев подобия при моделировании изучаемых процессов требует глубокого знания деталей этих процессов и в общем случае является очень трудной задачей. При решении этой задачи следует все изучаемые процессы разделить на две группы. К первой надо отнести процессы и явления, уже имеющие математическое описание. Ко второй, представляющей наибольший интерес, относятся процессы и явления, еще не имеющие математического описания. В тех случаях, когда уравнения исследуемых процессов неизвестны, единственной теорией, позволяющей найти числа подобия, является теория размерностей, которая в настоящей работе не рассматривается. При наличии дифференциальных уравнении исследуемых процессов числа подобия легко определяются как коэффициенты уравнений, представленных в безразмерном виде. Рассмотрим гидродинамическое подобие и подобие переноса тепла и вещества. При моделировании гидродинамических явлений должны быть соблюдены геометрическое, кинематическое и динамическое подобия. Соблюдение геометрического подобия означает, что модель подобна натуре, т. е. все сходственные линейные размеры исследуемой модели в одинаковое число раз меньше или больше, чем соответствующие размеры натуры. При этом не следует забывать о шероховатости поверхности. Кинематическое подобие означает, что безразмерные поля скоростей в рассматриваемых потоках одинаковы. Для выполнения динамического подобия двух потоков требуется, чтобы потоки описывались подобными дифференциальными уравнениями движения и имели подобные граничные условия. Для моделирования потоков жидкостей и газов и происходящих при этом процессов переноса тепла и вещества используют следующие безразмерные критерии подобия (для переноса тепла и переноса вещества эти числа будет соответственно называть тепловыми и диффузионными): Число Рейнольдса Число Эйлера Число Фруда Число Струхаля Число Фурье Число Архимеда
Число Прандтля тепловое диффузионное смешанное Число Нуссельта тепловое диффузионное где
Каждое из этих чисел характеризует условие подобия в зависимости от класса сил, действующих в потоке. Одинаковость чисел Re, Fu, Fr в подобных потоках означает соответственно равенство отношений сил вязкости, сил давления и массовых сил к силам инерции. Условие подобия по числам Sh и Fu имеет значение для неустановившегося движения. В случае движения сжимаемого газа число Eu можно представить в следующем виде:
где а — местная скорость звука, определяемая по формуле
где k — показатель адиабаты, равный отношению теплоемкости при постоянном давлении к теплоемкости при постоянном объеме ( Отношение скорости движения с к местной скорости звука а обычно обозначается через М= с / а – число Маха. Тогда формула (*) получается
Следовательно, для выполнения подобия с учетом сжимаемости необходимо, чтобы для модели и натуры числа М и Таким образом, если два потока жидкости динамически подобны, то для них должны соблюдаться следующие условия: Re1 = Re2; Fr1 = Fr2; причем индекс 1 относится к одному из рассматриваемых потоков, а индекс 2 — ко второму. При турбулентном движении жидкости в подобных потоках, помимо указанных чисел подобия, должны быть одинаковыми основные характеристики турбулентного потока: степень турбулентности и масштаб турбулентности.
|



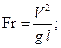
 (критерий гомохронности);
(критерий гомохронности);
 (
( и
и  - плотность частиц и плотность жидкости);
- плотность частиц и плотность жидкости);




 - характерная скорость, м/с;
- характерная скорость, м/с; - характерный размер, м;
- характерный размер, м; - кинематическая вязкость, м2/с;
- кинематическая вязкость, м2/с; - динамическая вязкость (
- динамическая вязкость ( ), Па·с;
), Па·с; - давление, Па;
- давление, Па; - ускорение свободного падения, 9.81 м/с2;
- ускорение свободного падения, 9.81 м/с2; - характерное время, с;
- характерное время, с; - разность удельных весов;
- разность удельных весов; - коэффициент температуропроводности;
- коэффициент температуропроводности;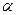 - коэффициент теплопередачи;
- коэффициент теплопередачи; - коэффициент переноса массы;
- коэффициент переноса массы; - коэффициент сопротивления;
- коэффициент сопротивления; - коэффициент диффузии.
- коэффициент диффузии.
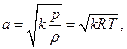
 ).
).
 были соответственно одинаковыми.
были соответственно одинаковыми. и М1 = М2,
и М1 = М2,


