Порядок выполнения работы. Возьмем числа 3, 6, 1. Их сумма равна 10.
Возьмем числа 3, 6, 1. Их сумма равна 10. Результат программы:
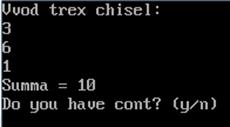
Возьмем числа -1, -3, -5. Их сумма равна -9. Результат программы:

Возьмем числа 5000, 4000, 2000. Их сумма равна 11000. Результат программы:
В нашей программе мы используем целочисленный тип данных у которых диапазон от -32000 до +32000. Таким образом, не отдельные величины, не а, b, с не должны превышать данные лимиты.
Лабораторная работа 1-2 ИЗУЧЕНИЕ КИНЕМАТИКИ И ДИНАМИКИ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ НА МАШИНЕ АТВУДА Цель работы:Экспериментальная проверка основных уравнений и законов поступательного движения тела. Теория Простейшей формой движения материи является механическое движение, которое состоит в перемещении тел или их частей друг относительно друга. Перемещения тел мы наблюдаем повседневно в обыденной жизни. Совокупность тел, выделенная для рассмотрения, называется механической системой. Какие тела следует включить в систему, зависит от характера решаемой задачи. Движение происходит как в пространстве, так и во времени. Поэтому для описания движения необходимо также определять время. Совокупность неподвижных друг относительно друга тел, по отношению к которым рассматривается движение, и отсчитывающих время часов образует систему отсчета. Описать движение тела означает указать для каждого момента времени положение в пространстве и скорость тела. Для того чтобы задать состояние механической системы, нужно указать положения и скорости всех тел, образующих систему. Типичная задача механики заключается в том, чтобы, зная состояние системы в некоторый начальный момент времени Отметим, что ни одна физическая задача не может быть решена абсолютно точно. Всегда получают приближенное решение. Степень приближение определяется характером задач, целью, которой хотят достичь. Решая задачу приближенно задачу, пренебрегают некоторыми факторами, которые в данном случае не существенны. Тело, размерами которого в условиях данной задачи можно пренебречь, называется материальной точкой. Одно и тоже тело в одних случаях может быть сочтено за материальную точку, в других же должно рассматриваться как протяженное тело. Говоря о каком-то теле как о материальной точке, мы абстрагируемся от его размеров. Вторая абстракция, с которой приходится иметь дело в механике, - это абсолютно твердое тело. Абсолютно твердым телом называется тело, деформациями которого можно в условиях данной задачи пренебречь. Всякое движение твердого тела можно разложить на два основных вида движения – поступательное и вращательное. Поступательное движение – это такое движение, при котором любая прямая, связанная с движущимся телом, остается параллельной самой себе. При вращательном движении все точки тела движутся по окружностям, центры которых, лежат на одной и той же прямой, называемой осью вращения. Для того чтобы получить возможность описывать движение количественно, приходится связывать с телами, образующими систему отсчета, какую-либо систему координат (например, декартовая система координат). Декартову систему координат рассматривают: В пространстве (трехмерный случай). При этом положение материальной точки A характеризуется тремя координатами: A(x, y, z). На плоскости (двумерный случай). При этом положение материальной точки A характеризуется двумя координатами: A(x, y). Движение материальной точки вдоль одной числовой прямой. При этом положение материальной точки A характеризуется только одной координатой: A(x).
При движении материальной точки в пространстве ее координаты с течением времени меняются. Поэтому положение материальной точки в любой момент времени определяется заданием функций Одним из первых разделов механики является кинематика, изучающая механическое движение тел без выяснения причин, вызывающих данное движение. Рассмотрим основные кинематические понятия траектория, путь и перемещение. Траектория – линия, описываемая в пространстве движущейся материальной точкой.
Перемещение (
где Быстрота изменения положения материальной точки в пространстве с течением времени характеризуется средней и мгновенной скоростями. Вектор средней скорости равен отношению перемещения к промежутку времени, за которое это перемещение произошло:
На рисунке 2 показано направление вектора средней скорости, которое совпадает с направлением перемещения Средняя скорость прохождения пути равна отношению пути к промежутку времени, за который этот путь пройден (средняя скорость – величина скалярная):
В момент времени t радиус-вектор задается тремя функциями: x(t), y(t) и z(t). В момент времени t+Dt значения функций станут равными: x(t+Dt), y(t+Dt) и z(t+Dt). Тогда приращения функций запишутся:
Эти приращения функций представляют собой компоненты вектора перемещения Вектор мгновенной скорости материальной точки, направленной по касательной к траектории движения (рис. 2) определяется как
Скорость частицы
Величина, определяемая формулой (6), называется ускорением частицы. Если Уравнения равнопеременного прямолинейного движения в векторной форме запишутся следующим образом:
где В скалярной форме (например, для проекции на ось 0x) уравнения записываются в следующем виде
Если проекции скорости или ускорения (для равноускоренного движения) соноправлены с осями 0x или 0y, то они считаются положительными; если антинаправлены, то – отрицательны, т.е. берутся со знаком «-». Если Уравнения равномерного прямолинейного движения в векторной форме запишутся следующим образом:
Уравнения (7) – (9) называются кинематическими уравнениями движения материальной точки. Уравнения движения рассматривают зависимость координат x, y, z от времени. Если из одного уравнения движения выразить время t и подставить в другое, то получим зависимость одних координат через другие. Геометрическое место последовательных положений материальной точки в пространстве называется траекторией точки. Положение точки задается ее координатами x и y (для случая плоского движения), которые при движении меняются со временем так что: Эти уравнения определяют закон движения материальной точки и представляют собой параметрические уравнения траектории точки. Выразив t через x и подставив t(x) в уравнение Кинематика дает описание движения тел, не затрагивая вопроса о том, почему тело движется именно так, а не иначе. Динамика изучает движение тел в связи с теми причинами (взаимодействиями между телами), которые обуславливают тот или иной характер движения. В основе так называемой классической или ньютоновской механики лежат три закона динамики, сформулированные Ньютоном в 1687г. Первый закон Ньютона формулируется следующим образом: всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние. Первый закон Ньютона выполняется только в инерциальных системах отсчета. Второй закон Ньютона гласит, что скорость изменения импульса тела равна действующей на тело силе:
где Уравнение (10) называется уравнением движения тела. Третий закон Ньютона утверждает, что силы, с которыми действуют друг на друга тела, равны по величине и противоположны по направлению: Несмотря на то, что основные уравнения кинематики и динамики прямолинейного движения имеют простую форму и не вызывают сомнения, экспериментальная проверка этих соотношений весьма сложна. Трудности возникают в основном по двум причинам. Во-первых, при достаточно больших скоростях движения тел необходимо с большой точностью измерять время их движения. Во-вторых, в любой системе движущихся тел действуют силы трения и сопротивления, которые трудно учесть с достаточной степенью точности. Определим, например, время падения тела с высоты h = 1,0 м при g равным 9,8 м/с2:
Если при выполнении эксперимента по определению g по времени падения тела с указанной высоты допускается погрешность в измерении времени равная 0,01 с, т. е. возможно получение значений времени 0,46 с или 0,44 с, разброс результатов измерений получается недопустимо большим: g=9,4 – 10,3 м/с2. С целью уменьшения влияния точности измерения времени на результаты измерений можно, например, резко увеличить высоту падения. Но при падении с больших высот достигаются большие скорости движения, что приводит к резкому увеличению сопротивления воздуха, которое трудно учесть. Трудности рассмотренного опыта связаны с большим значением ускорения свободного падения. Так как ускорение большое, то тело быстро набирает скорость, а при этом или время падения мало и его трудно точно измерить, или сама расчетная формула неточна, т. к. не учитывает трение. Уменьшить ускорение и одновременно максимально уменьшить силу сопротивления можно с помощью устройства, которое называют машиной Атвуда. Порядок выполнения работы Машина Атвуда (рис. 3) состоит из легкого блока Б, через который переброшена нить с двумя равными грузами на концах (масса обоих грузов одинакова и равна m). Грузы могут двигаться вдоль вертикальной рейки со шкалой Ш. Если на правый груз положить небольшой перегрузок, грузы начнут двигаться с некоторым ускорением. Кольцевая полочка П1, которая может закрепляться в любом положении, предназначена для свободного прохода груза и для снятия перегрузка. Для приема падающего груза служит полочка П2. Время движения грузов может измеряться с помощью ручного или стационарного секундомера.
Трение в машине Атвуда сведено к минимуму, но для возможно полной компенсации сил трения масса правого груза делается немного больше массы левого (с помощью дроби или пластилина). Операция балансировки, выполняется с таким расчетом, чтобы грузы не перевешивали друг друга, но от легкого толчка вниз правого груза вся система приходила в равномерное движение. (При расчетах можно считать массы грузов одинаковыми).
Второй закон Ньютона для каждого из тел системы в предположении невесомости блока и отсутствия трения дает
где Т1,2 – силы натяжения нити, m – масса каждого груза, Dm – масса перегрузка, а – ускорение системы. В проекциях на вертикальную ось ОY получаем соотношения
Отсюда, так как Т1 = Т2, ускорение движения системы равно
Из этого выражения видно, во-первых, что ускорение не зависит от времени, что доказывает равноускоренный характер движения грузов. Во-вторых, видно, что изменять ускорение можно, меняя массу перегрузка Dm. В случае равноускоренного движения скорость грузов v и их перемещение DS за время t определяются уравнениями
Так как начальная скорость в опытах на машине Атвуда обычно равна нулю и движение условно начинается из начала координат, то
Будем называть первое из этих соотношений законом скоростей, а второе законом перемещений. Соотношения (16) могут быть проверены экспериментально.
|


 , а также законы, управляющие движением, определить состояния системы во все последующие моменты времени
, а также законы, управляющие движением, определить состояния системы во все последующие моменты времени  .
. Для задания положения материальной точки в пространстве применяют понятие радиус-вектор
Для задания положения материальной точки в пространстве применяют понятие радиус-вектор  , как вектор, проведенный из начала системы координат O в точку нахождения материальной точки A (рис. 1)
, как вектор, проведенный из начала системы координат O в точку нахождения материальной точки A (рис. 1) ,
,  ,
,  , представляющих собой значения координат в момент времени t. Эти функции являются компонентами радиуса-вектора
, представляющих собой значения координат в момент времени t. Эти функции являются компонентами радиуса-вектора 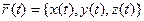 .
.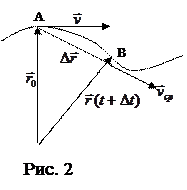 Путь (
Путь ( ) – расстояние межу двумя любыми точками, измеренное вдоль траектории (длина дуги траектории). Путь является скалярной величиной (рис. 2).
) – расстояние межу двумя любыми точками, измеренное вдоль траектории (длина дуги траектории). Путь является скалярной величиной (рис. 2). ) – вектор, соединяющий две точки траектории (вектор, соединяющий точки A и B, или разность двух радиусов-векторов
) – вектор, соединяющий две точки траектории (вектор, соединяющий точки A и B, или разность двух радиусов-векторов  и
и  ):
): (1)
(1) - радиус-вектор для момента времени t,
- радиус-вектор для момента времени t,  - радиус-вектор для момента времени
- радиус-вектор для момента времени  .
. (2)
(2) (3)
(3) (4)
(4) .
. (5)
(5)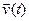 может изменяться со временем, как по величине, так и по направлению. Быстрота изменения вектора
может изменяться со временем, как по величине, так и по направлению. Быстрота изменения вектора  (6)
(6) и траектория – прямая линия, то движение равнопеременное прямолинейное.
и траектория – прямая линия, то движение равнопеременное прямолинейное. (7)
(7) – начальное положении материальной точки и
– начальное положении материальной точки и 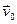 – начальная скорость.
– начальная скорость.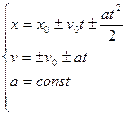 (8)
(8)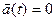 (
( ) и траектория – прямая линия, то движение равномерное прямолинейное.
) и траектория – прямая линия, то движение равномерное прямолинейное. (9)
(9) ,
,  .
. .
. (10)
(10) - импульс тела,
- импульс тела,  - действующая на тело сила.
- действующая на тело сила. .
. (11)
(11) Машина Атвуда может быть электрифицирована, т. е. снабжена электромагнитной муфтой-пускателем и автоматическим секундомером.
Машина Атвуда может быть электрифицирована, т. е. снабжена электромагнитной муфтой-пускателем и автоматическим секундомером.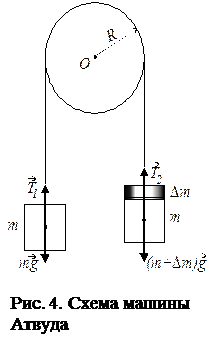 Для выполнения работы машина Атвуда должна быть установлена строго вертикально, что легко проверить по параллельности шкалы и нити. Кроме того, в тех опытах, где используется кольцевая полочка, положение ее должно быть отрегулировано так, чтобы грузы проходили через кольцо, не касаясь его, а перегрузок легко снимался и оставался на полочке.
Для выполнения работы машина Атвуда должна быть установлена строго вертикально, что легко проверить по параллельности шкалы и нити. Кроме того, в тех опытах, где используется кольцевая полочка, положение ее должно быть отрегулировано так, чтобы грузы проходили через кольцо, не касаясь его, а перегрузок легко снимался и оставался на полочке. , (12)
, (12) (13)
(13) (14)
(14) (15)
(15) (16)
(16)


