Метод контурных токов
1. Отчет 2. Диск с записью отчета и файлов: рисунки, схемы, MathCAD (xmcd) файлы, Excel (xlsx) файлы.
Решение Система уравнений по законам Кирхгофа Цепь содержит 6 ветвей и 4 узла. По первому закону Кирхгофа количество уравнений составляет Уравнения, составленные по первому закону Кирхгофа, для схемы на рисунке 1: Для узла «1» I3+I6-I5=0; Для узла «2» I1-I4-I6=0; Для узла «3» -I1-I2-I3=0. Уравнения, составленные по второму закону Кирхгофа, для схемы имеют вид: для контура «4214» I4R4-I6R6-I5R5=0; для контура «1231» I6R6+I1R1-I3R3=Е1-Е3; для контура «1341» I3R3-I2R2+I5R5= E3-E2.
В соответствии с заданной схемой и исходными данными система уравнений по законам Кирхгофа будет иметь вид:
Метод контурных токов При расчете методом контурных токов число необходимых уравнений определяется только выражением С учетом выбранного направления контурных токов составляется система из трех уравнений:
где R11, R22, R33 – собственные сопротивления соответственно 1, 2 и 3 контура (сумма сопротивлений всех ветвей, входящих в данный контур); R12=R21 – общее сопротивление контуров 1 и 2 (если направление контурных токов в общей ветви для контуров 1 и 2 совпадают, то R12 положительно, в противном случае R12 отрицательно); R13=R31 – общее сопротивление контуров 1 и 3; R23=R32 – общее сопротивление контуров 2 и 3; E nn - алгебраическая сумма ЭДС, включенных в ветви, образующие n-й контур.
R11=R4+R5+R6=2+2+6=10 Ом; R22=R1+R3+R6=5+8+6=19 Ом; R33=R2+R3+R5=2+8+2=12 Ом; R12= R21= -R6= -6 Ом; R13= R31=-R5=-2 Ом; R23= R32=-R3=-8 Ом;
E11=0 В; E22=Е1-Е3=14-28=-14 В; E33=Е3-Е2= 28-25= -3 В.
С учетом найденных значений система получает вид:
Решив составленную систему уравнений, например, методом Крамера, находим значения контурных токов I11, I22 и I33.
Через контурные токи определяются токи в ветвях:
|

 , а по второму
, а по второму 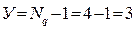 , где
, где 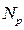 - количество ветвей,
- количество ветвей,  - количество узлов,
- количество узлов, 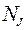 - количество ветвей с источниками тока.
- количество ветвей с источниками тока.

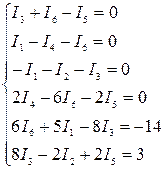
 .
.


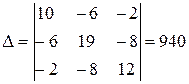


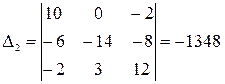



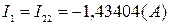 ;
; ;
; ;
; ;
; ;
; .
.


