Выберите марку авто
Постановка задачи: Метод контрольного объема:
(1)-Закон сохранения энергии
(1)-(2) –краевая задача
Точн. Приближенное значение температуры воды:
********
Надо найти Т(х), особенно
(1)- (2) –дифференциальная краевая задача (3)-(4) – разностная краевая задача Метод Томаса (прогонка) (3) записываем в стандартной форме
(5)- стандартная форма
(7) – подставляем в (5):

(5) = (7)È (8)
**
(7) -> i=n =>
Theorem: Если B>A+C, #include <iostream> #include <string> #include <cmath> #include <fstream>
using namespace std;
const double k = 0.6; // коэф. теплопроводности воды (Ватт/м*Кельвин) const double Cro = 4.094*1000; // коэф. теплоемкости трубы (Дж/кг*К) const double ro = 0.97; // плотрость воды (кг/м^3) const double u = 3; // скорость воды в трубе (м/с) const double H = 0.2; // толщина изоляций (м) const double V = 0.03; // коэф. теплопроводности стекловаты const double hc = V / H; // коэф. теплоотдачи в окруж. среду
const double R = 0.3; // радиус трубы (м) const int l = 5000; // длинна трубы (м) const int n = 1000; // число разбиений (м) const int Dx = l / n; // шаги
const int To = 95; // начальная температура
const double M = (ro*Cro*u) / k; const double N = (2*hc) / (R*k); double Alf[n],Bet[n],F[n],y[n],Tv1[n];
double Tv(double a){
if (a<=l/2) { return (48+((a - l/4) / (l/4)));} else { return (49+18*((a - l/2) / (l/4)));} } void GoToFile(double x) { ofstream file; file.open("results.txt", fstream::out | fstream::app); file<<x<<" "; file<<"\n";
file.close(); } int main (int argc, char *argv[]) { Alf[1] = 0; Bet[1] = To; y[0] = To;
double A = 1 + M*Dx; double B = 2 + M*Dx+N*Dx*Dx; double C = 1;
for(int i=1; i<n; i++){ F[i] = N*Dx*Dx*Tv(i*Dx); } for(int i = 1; i < n; i++){ Alf[i+1] = A / (B - C*Alf[i]); Bet[i+1] = (C*Bet[i] + F[i]) / (B - C*Alf[i]); }
y[n] = Bet[n] / (1 - Alf[n]); for(int i = n; i > 1; i--){ y[i-1] = Alf[i]*y[i] + Bet[i]; }
for(int i=0; i<=n; i++){ cout<<y[i]<<"\t"<<y[l/2+i]<<endl; if (i==l/2+1) break; if(i%2 ==0) GoToFile(y[i]);
//GoToFile(Tv(i*Dx)); }
system("pause"); return 0; }
Вывод: Если у меня начальная температура Т0 = 95 и при линейной интерполяции -Тв = 48 при х=l/4 -Тв = 49 при х=l/2 -Тв = 67 при х=3l/4
Вариант 1. Вычислите: arcsin ( 1) 2. Вычислите: arcos ( 1) 3. Решите уравнение: sin x - 1) 4. Решите уравнение: cos 2x=1 1) 5. Укажите уравнение, которому соответствует решение: 1) tg x = 1; 2) cos x = 0; 3) sin x = -1; 4) ctg x = 6. На каком из рисунков показано решение неравенства: cos x < 1) 2) 3) 4)
7. Решите неравенство: tg x ≥ 1) 8. Решите уравнение: 6sin2 x + sin x – 1 = 0 1) 9. Решите уравнение: 2sin2 x - 10. Решите систему:
Выберите марку авто
Ssang Yong
Subaru
Suzuki
Toyota
Volkswagen
Volvo
|





 (2)
(2)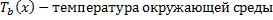
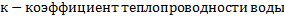





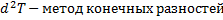
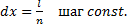
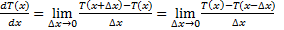
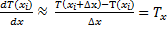 - правая разностная
- правая разностная - левая разностная
- левая разностная
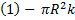
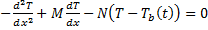
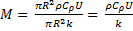
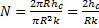





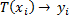


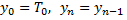

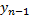

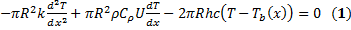






 (4)
(4)




 (7)
(7)

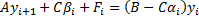



 это равенство выполняется для любого
это равенство выполняется для любого 




 то все
то все 
 ;
;
 ) + 2arctg(-1)
) + 2arctg(-1) ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
. ) + 2arcctg(
) + 2arcctg( )
) ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
. =0
=0 2)
2)  ; 3)
; 3)  4)
4) 
 2)
2)  3)
3)  4)
4) 
 :
: .
.
 2)
2)  3)
3)  4)
4) 
 3) нет корней; 4)
3) нет корней; 4)  .
.
 Alfa Romeo
Alfa Romeo  Dodge
Dodge  Jeep
Jeep  Mitsubishi
Mitsubishi Aston Martin
Aston Martin  Ferrari
Ferrari  Kia
Kia  Nissan
Nissan Audi
Audi  Fiat
Fiat  Lancia
Lancia  Opel
Opel
 Bentley
Bentley  Ford
Ford  Land Rover
Land Rover  Peugeot
Peugeot
 BMW
BMW  Gmc
Gmc  Lexus
Lexus  Pontiac
Pontiac
 Cadillac
Cadillac  Honda
Honda  Lincon
Lincon  Porsche
Porsche
 Chevrolet
Chevrolet  Hummer
Hummer  Lotus
Lotus  Renault
Renault
 Chrysler
Chrysler  Hyundai
Hyundai  Maserati
Maserati  Rover
Rover
 Citroen
Citroen  Infiniti
Infiniti  Mazda
Mazda  Saab
Saab Dacia
Dacia  Isuzu
Isuzu  Mercedes
Mercedes  Seat
Seat Daewoo
Daewoo  Iveco
Iveco  MG
MG  Skoda
Skoda Daihatsu
Daihatsu  Jaguar
Jaguar  Mini
Mini  Smart
Smart


