7. Задание 3 № 27581.  Найдите площадь закрашенной фигуры на координатной плоскости.
Найдите площадь закрашенной фигуры на координатной плоскости.
8. Задание 3 № 27647.  Из точки А (6; 8) опущен перпендикуляр на ось абсцисс. Найдите абсциссу основания перпендикуляра.
Из точки А (6; 8) опущен перпендикуляр на ось абсцисс. Найдите абсциссу основания перпендикуляра.
9. Задание 3 № 27648.  Через точку А (6; 8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью Oy.
Через точку А (6; 8) проведена прямая, параллельная оси абсцисс. Найдите ординату ее точки пересечения с осью Oy.
10. Задание 3 № 27649.  Найдите расстояние от точки A с координатами (6; 8) до оси абсцисс.
Найдите расстояние от точки A с координатами (6; 8) до оси абсцисс.
13. Задание 3 № 27652. 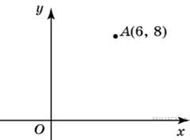 Найдите абсциссу точки, симметричной точке A (6; 8) относительно оси Oy.
Найдите абсциссу точки, симметричной точке A (6; 8) относительно оси Oy.
16. Задание 3 № 27655.  Найдите ординату точки, симметричной точке A (6; 8) относительно начала координат.
Найдите ординату точки, симметричной точке A (6; 8) относительно начала координат.
17. Задание 3 № 27656.  Найдите ординату середины отрезка, соединяющего точки O (0; 0) и A (6; 8).
Найдите ординату середины отрезка, соединяющего точки O (0; 0) и A (6; 8).
21. Задание 3 № 27660.  Найдите ординату точки пересечения оси Oy и отрезка, соединяющего точки A (6; 8) и B (−6; 0).
Найдите ординату точки пересечения оси Oy и отрезка, соединяющего точки A (6; 8) и B (−6; 0).
24. Задание 3 № 27665.  Найдите синус угла наклона отрезка, соединяющего точки O (0; 0) и A (6; 8), с осью абсцисс.
Найдите синус угла наклона отрезка, соединяющего точки O (0; 0) и A (6; 8), с осью абсцисс.
25. Задание 3 № 27666.  Найдите косинус угла наклона отрезка, соединяющего точки O (0; 0) и A (6; 8), с осью абсцисс.
Найдите косинус угла наклона отрезка, соединяющего точки O (0; 0) и A (6; 8), с осью абсцисс.
26. Задание 3 № 27667.  Найдите угловой коэффициент прямой, проходящей через точки с координатами (−2; 0) и (0; 2).
Найдите угловой коэффициент прямой, проходящей через точки с координатами (−2; 0) и (0; 2).
28. Задание 3 № 27669. 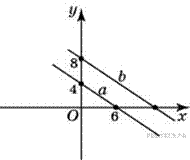 Прямая a проходит через точки с координатами (0; 4) и (6; 0). Прямая b проходит через точку с координатами (0; 8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox
Прямая a проходит через точки с координатами (0; 4) и (6; 0). Прямая b проходит через точку с координатами (0; 8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox
31. Задание 3 № 27672.  Точки O (0; 0), B (6; 2), C (0; 6) и A являются вершинами параллелограмма. Найдите ординату точки A.
Точки O (0; 0), B (6; 2), C (0; 6) и A являются вершинами параллелограмма. Найдите ординату точки A.
34. Задание 3 № 27675.  Точки O (0; 0), A (6; 8), B (6; 2), C (0; 6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей.
Точки O (0; 0), A (6; 8), B (6; 2), C (0; 6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей.
44. Задание 3 № 27685.  Точки O (0; 0), A (6; 8), B (8; 2) являются вершинами треугольника. Найдите длину его средней линии CD, параллельной OA.
Точки O (0; 0), A (6; 8), B (8; 2) являются вершинами треугольника. Найдите длину его средней линии CD, параллельной OA.
45. Задание 3 № 27686.  Точки O (0; 0), A (10; 0), B (8; 6), C (2; 6) являются вершинами трапеции. Найдите длину ее средней линии DE.
Точки O (0; 0), A (10; 0), B (8; 6), C (2; 6) являются вершинами трапеции. Найдите длину ее средней линии DE.
46. Задание 3 № 27687.  Найдите абсциссу точки пересечения прямой, заданной уравнением 3 x + 2 y = 6, с осью Ox.
Найдите абсциссу точки пересечения прямой, заданной уравнением 3 x + 2 y = 6, с осью Ox.
48. Задание 3 № 27689.  Найдите абсциссу точки пересечения прямых, заданных уравнениями 3 x + 2 y = 6 и y = x.
Найдите абсциссу точки пересечения прямых, заданных уравнениями 3 x + 2 y = 6 и y = x.
49. Задание 3 № 27690.  Найдите ординату точки пересечения прямых, заданных уравнениями 3 x + 2 y = 6 и y = − x.
Найдите ординату точки пересечения прямых, заданных уравнениями 3 x + 2 y = 6 и y = − x.
51. Задание 3 № 27692.  Окружность с центром в начале координат проходит через точку P (8; 6). Найдите ее радиус.
Окружность с центром в начале координат проходит через точку P (8; 6). Найдите ее радиус.
52. Задание 3 № 27693.  Какого радиуса должна быть окружность с центром в точке P (8; 6), чтобы она касалась оси абсцисс?
Какого радиуса должна быть окружность с центром в точке P (8; 6), чтобы она касалась оси абсцисс?
54. Задание 3 № 27695.  Найдите радиус окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (−2; −2), (6; −2), (6; 4), (−2; 4).
Найдите радиус окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (−2; −2), (6; −2), (6; 4), (−2; 4).
57. Задание 3 № 27698.  Найдите радиус окружности, описанной около треугольника, вершины которого имеют координаты (8; 0), (0; 6), (8; 6).
Найдите радиус окружности, описанной около треугольника, вершины которого имеют координаты (8; 0), (0; 6), (8; 6).
58. Задание 3 № 27699.  Найдите абсциссу центра окружности, описанной около треугольника, вершины которого имеют координаты (8; 0), (0; 6), (8; 6).
Найдите абсциссу центра окружности, описанной около треугольника, вершины которого имеют координаты (8; 0), (0; 6), (8; 6).

 Найдите площадь закрашенной фигуры на координатной плоскости.
Найдите площадь закрашенной фигуры на координатной плоскости. Из точки А (6; 8) опущен перпендикуляр на ось абсцисс. Найдите абсциссу основания перпендикуляра.
Из точки А (6; 8) опущен перпендикуляр на ось абсцисс. Найдите абсциссу основания перпендикуляра. Найдите абсциссу точки, симметричной точке A (6; 8) относительно оси Oy.
Найдите абсциссу точки, симметричной точке A (6; 8) относительно оси Oy. Найдите ординату середины отрезка, соединяющего точки O (0; 0) и A (6; 8).
Найдите ординату середины отрезка, соединяющего точки O (0; 0) и A (6; 8). Найдите ординату точки пересечения оси Oy и отрезка, соединяющего точки A (6; 8) и B (−6; 0).
Найдите ординату точки пересечения оси Oy и отрезка, соединяющего точки A (6; 8) и B (−6; 0). Найдите синус угла наклона отрезка, соединяющего точки O (0; 0) и A (6; 8), с осью абсцисс.
Найдите синус угла наклона отрезка, соединяющего точки O (0; 0) и A (6; 8), с осью абсцисс. Найдите угловой коэффициент прямой, проходящей через точки с координатами (−2; 0) и (0; 2).
Найдите угловой коэффициент прямой, проходящей через точки с координатами (−2; 0) и (0; 2). Прямая a проходит через точки с координатами (0; 4) и (6; 0). Прямая b проходит через точку с координатами (0; 8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox
Прямая a проходит через точки с координатами (0; 4) и (6; 0). Прямая b проходит через точку с координатами (0; 8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox Точки O (0; 0), B (6; 2), C (0; 6) и A являются вершинами параллелограмма. Найдите ординату точки A.
Точки O (0; 0), B (6; 2), C (0; 6) и A являются вершинами параллелограмма. Найдите ординату точки A. Точки O (0; 0), A (6; 8), B (6; 2), C (0; 6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей.
Точки O (0; 0), A (6; 8), B (6; 2), C (0; 6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей. Точки O (0; 0), A (6; 8), B (8; 2) являются вершинами треугольника. Найдите длину его средней линии CD, параллельной OA.
Точки O (0; 0), A (6; 8), B (8; 2) являются вершинами треугольника. Найдите длину его средней линии CD, параллельной OA. Точки O (0; 0), A (10; 0), B (8; 6), C (2; 6) являются вершинами трапеции. Найдите длину ее средней линии DE.
Точки O (0; 0), A (10; 0), B (8; 6), C (2; 6) являются вершинами трапеции. Найдите длину ее средней линии DE. Найдите абсциссу точки пересечения прямой, заданной уравнением 3 x + 2 y = 6, с осью Ox.
Найдите абсциссу точки пересечения прямой, заданной уравнением 3 x + 2 y = 6, с осью Ox. Найдите абсциссу точки пересечения прямых, заданных уравнениями 3 x + 2 y = 6 и y = x.
Найдите абсциссу точки пересечения прямых, заданных уравнениями 3 x + 2 y = 6 и y = x. Найдите ординату точки пересечения прямых, заданных уравнениями 3 x + 2 y = 6 и y = − x.
Найдите ординату точки пересечения прямых, заданных уравнениями 3 x + 2 y = 6 и y = − x. Окружность с центром в начале координат проходит через точку P (8; 6). Найдите ее радиус.
Окружность с центром в начале координат проходит через точку P (8; 6). Найдите ее радиус. Найдите радиус окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (−2; −2), (6; −2), (6; 4), (−2; 4).
Найдите радиус окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (−2; −2), (6; −2), (6; 4), (−2; 4). Найдите радиус окружности, описанной около треугольника, вершины которого имеют координаты (8; 0), (0; 6), (8; 6).
Найдите радиус окружности, описанной около треугольника, вершины которого имеют координаты (8; 0), (0; 6), (8; 6).


