| №
| Содержание операции
| Сумма
| Проводка
|
| дебет
| Кредит
|
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
| | | | | |
Вариант 1
Задача 15.
1. Решите уравнение  ;
;
2. Найдите все корни данного уравнения, принадлежащие промежутку 
Решение.
1. Введя замену  , получим квадратное уравнение
, получим квадратное уравнение  с корнями
с корнями  и
и  . Первый корень следует исключить, так как для любого угла его синус по модулю не превосходит 1.
. Первый корень следует исключить, так как для любого угла его синус по модулю не превосходит 1.
Тогда
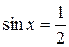 ,
,  (
( ),
), 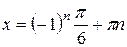 (
( ).
).
2. Выберем корни, принадлежащие отрезку  . Получим:
. Получим:  и
и  Ответ: а)
Ответ: а) 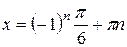 (
( ), б)
), б)  и
и  .
.
| Содержание критерия
| Баллы
|
| Обоснованно получены ответы в обоих пунктах
|
|
| Обоснованно получен верный ответ в пункте а или пункте б,
ИЛИ
получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения уравнения и отбора корней
|
|
| Решение не соответствует ни одному из критериев, приведённых выше
|
|
| Максимальный бал
|
|
Задача 16. В правильной шестиугольной призме  ,...,
,...,  все ребра равны 1.
все ребра равны 1.
1. Постройте сечение призмы плоскостью, проходящей через точки 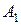 ,
, 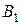 и. С
и. С
2. Найдите расстояние от точки  до прямой
до прямой  .
.
Решение.
1. Прямая  ‑ пересечение сечения с плоскостью
‑ пересечение сечения с плоскостью  . Так как прямые
. Так как прямые  и
и  параллельны, то и содержащие их плоскости будут пересекаться по прямой, параллельной прямым
параллельны, то и содержащие их плоскости будут пересекаться по прямой, параллельной прямым  и
и  . Тогда для получения пересечения сечения с плоскостью
. Тогда для получения пересечения сечения с плоскостью 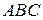 , проведем прямую через точку
, проведем прямую через точку  , параллельную прямой
, параллельную прямой  . При этом получим прямую
. При этом получим прямую 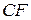 .
.  ‑ искомое сечение.
‑ искомое сечение.

2. Из прямоугольного треугольника  по теореме Пифагора имеем
по теореме Пифагора имеем
 .
.

Так как имеем равнобочную трапецию, то
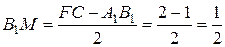 .
.
Из прямоугольного треугольника  по теореме Пифагора получим, что искомое расстояние равно
по теореме Пифагора получим, что искомое расстояние равно
 .
.

 ;
;
 , получим квадратное уравнение
, получим квадратное уравнение  с корнями
с корнями  и
и  . Первый корень следует исключить, так как для любого угла его синус по модулю не превосходит 1.
. Первый корень следует исключить, так как для любого угла его синус по модулю не превосходит 1.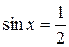 ,
,  (
( ),
), 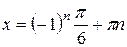 (
( и
и  Ответ: а)
Ответ: а)  ,...,
,...,  все ребра равны 1.
все ребра равны 1.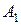 ,
, 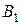 и. С
и. С до прямой
до прямой  .
. ‑ пересечение сечения с плоскостью
‑ пересечение сечения с плоскостью  . Так как прямые
. Так как прямые  и
и 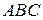 , проведем прямую через точку
, проведем прямую через точку 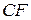 .
.  ‑ искомое сечение.
‑ искомое сечение.
 по теореме Пифагора имеем
по теореме Пифагора имеем .
.
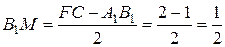 .
. по теореме Пифагора получим, что искомое расстояние равно
по теореме Пифагора получим, что искомое расстояние равно .
.


