| Содержание критерия
| Баллы
|
| Обоснованно получен верный ответ
|
|
| С помощью верного рассуждения получено множество значений a, отличающееся от искомого только включением точек a = -11 и/или а= –1
|
|
| Задача сведена к решению двойного неравенства, но решение не доведено о конца
|
|
| Показано только, что единица всегда принадлежит области значений функции
|
|
| Решение не соответствует ни одному из критериев, приведённых выше
|
|
| Максимальный бал
|
|
Задача 21. На доске написано более 27, но менее 45 целых чисел. Среднее арифметическое этих чисел равно -5, среднее арифметическое всех положительных из них равно 9, а среднее арифметическое всех отрицательных из них равно -18.
а) Сколько чисел написано на доске?
б) Каких чисел написано больше: положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди них?
Решение: Пусть среди написанных чисел  положительных,
положительных,  отрицательных и
отрицательных и  нулей. Сумма набора чисел равна количеству чисел в этом наборе, умноженному на его среднее арифметическое, поэтому
нулей. Сумма набора чисел равна количеству чисел в этом наборе, умноженному на его среднее арифметическое, поэтому 
а) Заметим, что в левой части каждое слагаемое делится на 9, поэтому  - количество целых чисел - делится на 9. По условию
- количество целых чисел - делится на 9. По условию 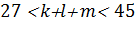 , поэтому
, поэтому  . Таким образом, написано 36 чисел.
. Таким образом, написано 36 чисел.
б) Приведём равенство  к виду
к виду  Так как
Так как  , получаем, что
, получаем, что 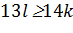 , откуда
, откуда  . Следовательно, отрицательных чисел больше, чем положительных.
. Следовательно, отрицательных чисел больше, чем положительных.
в(оценка) Подставим  в правую часть равенства
в правую часть равенства  , откуда
, откуда  . Так как
. Так как  , получаем:
, получаем:  то есть положительных чисел не более 16.
то есть положительных чисел не более 16.
в(пример) Приведём пример, когда положительных чисел ровно 16. Пусть на доске 16 раз написано число 9, 18 раз написано число -18 и два раза написан 0. Тогда

указанный набор удовлетворяет всем условиям задачи.
Ответ: а)36; б) отрицательных; в)16.
| Содержание критерия
| Баллы
|
| Верно выполнены: а, б, в(пример), в(оценка)
|
|
| Верно выполнены три пункта из четырёх: а, б, в(пример), в(оценка)
|
|
| Верно выполнены два пункта из четырёх: а, б, в(пример), в(оценка)
|
|
| Верно выполнен один пункт из четырёх: а, б, в(пример), в(оценка)
|
|
| Решение не соответствует ни одному из критериев, перечисленных выше
|
|
| Максимальный бал
|
|

 положительных,
положительных,  отрицательных и
отрицательных и  нулей. Сумма набора чисел равна количеству чисел в этом наборе, умноженному на его среднее арифметическое, поэтому
нулей. Сумма набора чисел равна количеству чисел в этом наборе, умноженному на его среднее арифметическое, поэтому 
 - количество целых чисел - делится на 9. По условию
- количество целых чисел - делится на 9. По условию 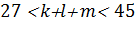 , поэтому
, поэтому  . Таким образом, написано 36 чисел.
. Таким образом, написано 36 чисел. к виду
к виду  Так как
Так как  , получаем, что
, получаем, что 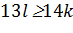 , откуда
, откуда  . Следовательно, отрицательных чисел больше, чем положительных.
. Следовательно, отрицательных чисел больше, чем положительных. , откуда
, откуда  . Так как
. Так как  , получаем:
, получаем:  то есть положительных чисел не более 16.
то есть положительных чисел не более 16.



