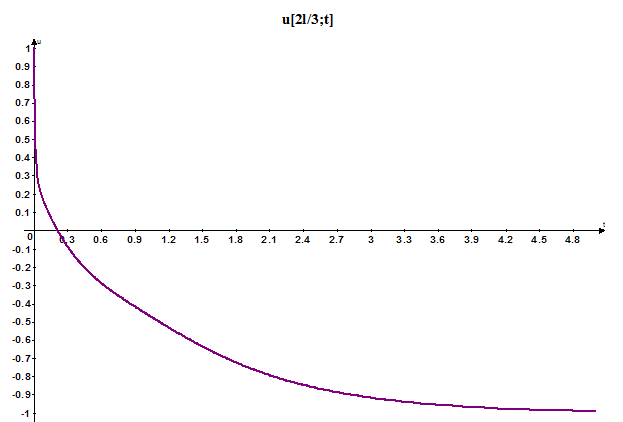
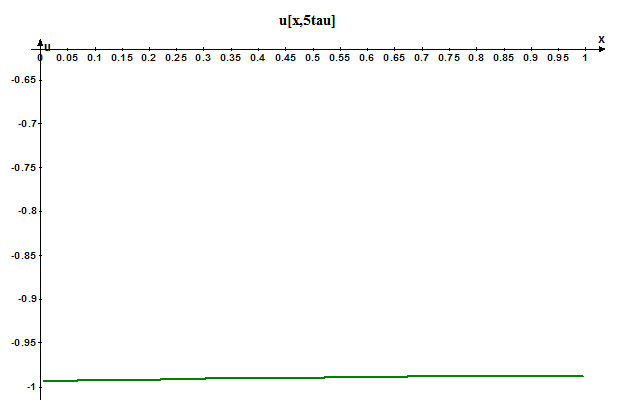
Задание 3. Метод Кранка-Николсона

 

В методе Кранка-Николсона экспоненциал матрицы и интеграл аппроксимируются с большей точностью, чем в методе Эйлера:

Подставляя данные выражения в уравнение, получим:

 

 

Умножая слева на получаем:

 

Выражение в правой части считается явно, чтобы найти v(t+dt) нужно дважды решить систему линейных алгебраических уравненений. Это делается методом прогонки.

 

Исходный код программы:

 

#include<iostream>

#include<math.h>

#include<cstdlib>

#include<cstdio>

 

using namespace std;

 

#define sqr(x) ((x) * (x))

 

const int Nx = 40;

const double Nt = 6000;

 

 

double alpha, beta; double dx;

 

double a [Nx], b [Nx], c[Nx];

 

//Умножение вектора u на матрицу (E + lambda*A):

void matrix(double *u, double lambda) {

 

double dx = 1 / double(Nx);

double alpha = -1.0;

double beta = -2.0 + (1 - dx / 2) / (1 + dx / 2);

 

double v [Nx];

for (int i=1; i<Nx-1; i++) {

v[i] = u[i] + lambda * (u[i - 1] - 2.0 * u[i] + u[i + 1]) /sqr(dx) * D;

 

}

v[0] = u[0] + lambda * (beta * u[0] - u[1]) /sqr (dx) * D;

v[Nx - 1] = u[Nx - 1] + lambda * (u[Nx - 2] + u[Nx - 1] * alpha) /sqr (dx) * D;

 

for (int i = 0; i < Nx; i++) u[i] = v[i];

}

 

//Метод прогонки:

void sweep(double *u) {

for (int j = 0; j < Nx - 1; j++){

 

double w = b[j] / a[j];

a[j + 1] -= c[j] * w;

u[j + 1] -= u[j] * w;

}

for (int j = Nx - 1; j > 0; j--) {

double w = c[j - 1] / a[j];

u[j - 1] -= u[j] * w;

u[j] /= a[j];

}

u[0] /= a[0];

}

 

 

int main() {

 

double l=1, tau=1;

double xx = 2 * l / 3.0;

double tt = 5 * tau; //момент выхода из цикла по t

double dx = 1 / double(Nx);

double dt = tau / Nt;

double alpha = -1.0;

double beta = -2.0 + (1 - dx / 2) / (1 + dx / 2);

double D = sqr(l) / tau;

 

double u[Nx];

 

 

//задание начальных условий:

for (int i = 0; i < Nx; i++) {

u[i] = fabs((i + 0.5) * dx - (2*l/3.0)) < l / 10.0? 1.0: 0.0;

}

 

freopen("krahk_nicholson_t", "w", stdout);

 

int Ntt = tt / dt;

 

//Вычисление u в точке 2*l/3:

for (int i = 0; i < Ntt; i++) {

if (i < Nt)

cout << dt * i << " " <<

u[(int) (xx / l * double(Nx))] - (1 - exp(-i * dt / tau))<< '\n';

 

 

double q = 1.0 / tau * exp(-1 * i * dt / tau); //источник тепла в уравнении

double qq = exp(-1 * dt / tau);

 

 

//Вычисление правой части основной формулы:

double v[Nx], w[Nx], p[Nx];

for (int j = 0; j < Nx; j++) v[j] = u[j]; //v(t)

matrix(v, dt / 2);

matrix(v, dt / 2);

 

for (int j = 0; j < Nx; j++) w[j] = qq * q * dt / 2.0; //q(t+dt)

matrix(w, -dt / 2);

matrix(w, -dt / 2);

 

for (int j = 0; j < Nx; j++) p[j] = q * dt / 2.0; //q(t)

matrix(p, -dt / 2);

matrix(p, dt / 2);

 

 

for (int j = 0; j < Nx; j++) v[j] += w[j] + p[j];

 

//вычисление коэффициентов трехдиагональной матрицы:

for (int j = 0; j < Nx - 1; j++) {

a[j] = 1.0 + dt / sqr(dx) * D; b [ j ] = c [j] = -dt / sqr(dx) / 2 * D;

}

a[0] = 1 - dt * beta / 2 / sqr(dx) * D;

a[Nx - 1] = 1 - dt * alpha / 2 / sqr(dx) * D;

 

sweep(v);

 

//вычисление коэффициентов трехдиагональной матрицы:

for (int j = 0; j < Nx - 1; j++) {

a[j] = 1.0 - dt / sqr(dx) * D; b [j] = c [j] = +dt / sqr(dx) / 2 * D;

}

a[0] = 1 + dt * beta / 2 / sqr(dx) * D;

a[Nx - 1] = 1 + dt * alpha / 2 / sqr(dx) * D;

 

sweep(v);

 

 

for (int j = 0; j < Nx; j++) u[j] = v[j];

}

 

 

freopen("krank_nicholson_x", "w", stdout);

 

// зависимость от x:

 

for (int i = 0; i < Nx; i++) {

 

cout << (i + 0.5) * dx << " " << u[i] - (1 - exp(- 1.0 * tt / tau)) << "\n";

}

 

return 0;

 

}

 

При построении данных графиков для обеспечения устойчивости нам хватило Nx=40; Ny=6000.

 

 

 

 

Вывод:

Мы получили решение исходной задачи тремя методами. Графики решений соответствуют физическому смыслу задачи и достаточно хорошо соответствуют друг другу.

Метод суммирования ряда Фурье самый простой по сложности реализации и самый быстрый, но он требует полного аналитического решения задачи, и в этом смысле достаточно трудоемкий. Он вполне годится для построения графиков уже известных решений.

Явный метод Эйлера и метод Кранка-Николсона более сложны в написании и работают медленнее, особенно метод Кранка-Николсона, требующий большого количества вычислений на каждом шаге, но эти методы не требуют знания решения уравнения. Они также позволяют построить график решения с требуемой точностью. Пожалуй, самым эффективным является явный метод Эйлера, так как он требует гораздо меньше вычислений, чем метод Кранка-Николсона, хотя количество разбиений по времени в нем гораздо больше, и дает вполне приемлемую точность. Метод Кранка-Николсона гораздо более дорогой, но он обеспечивает нам безусловно устойчивое решение при достаточно малом количестве точек разбиения по времени.