Работа по вычислительной математике
Метод хирургической работы, обеспечивающий предупреждение попадания микробов в операционную рану или развития их в ней. На всех окружающих человека предметах, в воздухе, в воде, на поверхности его тела, в содержимом внутренних органов и т.д. имеются бактерии. Поэтому хирургическая работа требует соблюдения основного закона асептики, который формулируется так: все, что приходит в соприкосновение с раной, должно быть свободно от бактерий, т.е. стерильно. Асептика обладает несомненными преимуществами перед антисептикой в смысле результатов лечения, а также потому, что при асептическом способе лечения ран не бывает отравлений, которые возможны при применении некоторых антисептических средств. Асептика - это совокупность методов и приемов работы, направленных на предупреждение попадания инфекции в рану, в организм больного, создание безмикробных, стерильных условий для всей хирургической работы путем использования организационных мероприятий, активных обеззараживающих химических веществ, а также технических средств и физических факторов. Таким образом, если антисептика уничтожает микроорганизмы в организме пациента, то асептика предупреждает их попадание в рану, организм больного. Работа по вычислительной математике Работу выполняли: Лазаревич, Разумов, Селезнёв, Сысоев Задание: Тремя способами численно решить уравнение теплопроводности (1) с заданными граничными (2) и начальными (3) условиями.
Результаты представить в виде графиков:
Часть 1. Решение методом Фурье Переведём неоднородность(2.2) в уравнение, для этого представим u в виде (4)
Подставим u из (4) в уравнение (1), получим уравнение с источником (5) на w
С однородными граничными условиями (6.1) и (6.2):
И таким же, как для u начальным условием (7):
Будем решать задачу 5-6-7 Найдём собственные функции
Обозначим Разложим по собственным функциям q(x,t).
Будем искать решение
Из единственности разложения (в том числе и нуля) по собственным функциям следует:
Найдем частное неоднородного
Ответ:
где Наглядное графическое решение уравнения 6:
y=x – красная линия, y=ctgx – зеленая, построены в Advanced Grapher’е Также видно, что отрицательные корни
Таблица некоторых значений корней уравнения x=ctgx:
Оценим остаток ряда
Если взять всего 20 членов ряда, то остаток будет меньше Второй ряд (относящийся ко второй части
Исходный код программы: #include <stdio.h> #include <math.h> #include <iostream> #include <fstream>
using namespace std; const double PI=3.1415926535897932384626433832795; const double l=1; const double tau=1; const int Nx=100; //число точек разбиения по х const int Nt=100; // число точек разбиения по t const int s=2; // s=2 или s=5 const int n=20; //колличество членов ряда #define sqr(x) (x*x)
double f(double pk) //для поиска собственных значений { return pk*tan(pk)-1; }
double ser(double pk,double t, double x)// член ряда bk(t)*Xk(x) { double z=sin(pk)/(1-pk*pk); double y=4/(2*pk+sin(2*pk)); double bk=y*(z*exp(-t/tau)+(2*cos(pk/3)*sin(pk/10)-z)*exp(-sqr(pk)*t/tau)); return bk*cos(pk*(x/l-1)); }
double sup(double t) //добавок к решению { return exp(-t/tau)-1; }
double q; //корень метода деления пополам
int main() { ofstream out("Tables.txt"); //вывод таблиц в файл out<<"k"<<'\t'<<"pk"<<'\n'; double a,b; //концы отрезков, на которых будем искать корни double p[n];//корни уравнения x=ctgx for (int i=1;i<n+1;i++)//поиск корней уравнения x*tan(x)-1 методом деления пополам { a=1.000001*PI*(i-1); b=0.99999*(2*i-1)*(PI/2);
while ((abs(b-a)>0.0001)&&(f(q)!=0)) { q=(a+b)/2; if (f(a)*f(q)>0) a=q; if (f(a)*f(q)<0) b=q; } p[i-1]=q;//заполняем массив корней out<<i-1<<'\t'<<p[i-1]<<'\t'<<'\n'; // напечатаем корни в таблицу }
double dx=l/Nx; double dt=tau/Nt; out<<" "<<"x"<<" "<<"u[x,k*tau]:"<<'\n'; double v[Nx]; for(int i=0;i<Nx;i++) v[i]=0; for(int i=0;i<Nx;i++) // заполняем U(x,s*tau) { for(int j=0;j<n;j++) //cуммирование n членов ряда v[i]=v[i]+ser(p[j],s*tau,i*dx); out<<i*dx<<'\t'<<v[i]+sup(s*tau)<<'\n'; //вывод u[i*d,s*tau] }
out<<'\n'<<" "<<"t"<<" "<<"u[2l/3,t]:"<<'\n'; double u[5*Nt]; for(int i=0;i<5*Nt;i++) // заполняем U(2l/3,t) u[i]=0; for(int i=0;i<5*Nt;i++) { for(int j=0;j<n;j++) u[i]=u[i]+ser(p[j],i*dt,2*l/3); out<<i*dt<<'\t'<<u[i]+sup(i*dt)<<'\n'; } return 0;
}
Нам заранее неизвестно, как будут выглядеть графики при s=2 и s=5 (говоря на языке программы). Про график u(2l/3,t) мы знаем, что он должен выходить из единицы. И мы точно знаем, как будет выглядеть график при s=0, а именно: он должен быть похож на начальное условие. Правда, при t=0 ряд
сходится хуже всего.
Начальное условие. При Nx=300 – число точек разбиения отрезка [0;l], и n=20 и n=40 - число членов ряда. Двадцати членов ряда должно хватить для решения нашей задачи. А соответствие начальным условиям говорит в пользу, того что мы не ошиблись, пока решали задачу на бумаге и писали программу.
Построим графики для метода Фурье. 1) График при x*=2l/3. Nt=100 - количество точек на отрезке [0;τ] (при большем Nt уже не видно разницы); n=20, как мы и оценивали.
2) Nx=100 (если их больше, то не видно разницы, правда, если меньше, то разница тоже не особо заметна). Вообще Nx подбирается так, чтобы было учтено изменение последнего члена ряда. n=20.
3)Nx=100; n=20
При T=5τ температура от координаты меняется еще незаметнее. Вообще, в любой точке x стержня при t→∞ решение стремиться к постоянному значению u=-1, и такая динамика здесь прослеживается.
|





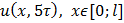 ;
;  .
.

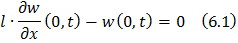




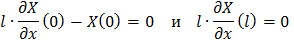

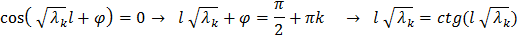
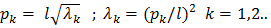
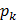 – безразмерный коэффициент
– безразмерный коэффициент





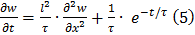 в виде (11)
в виде (11) 

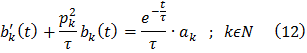
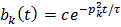 – общее решение однородного.
– общее решение однородного.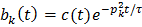 вариацией произвольной постоянной.
вариацией произвольной постоянной.






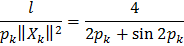
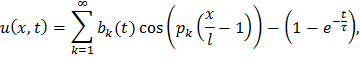
 положительные корни уравнения (6)
положительные корни уравнения (6) 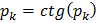 .
.
 , и им отвечают те же собственные функции.
, и им отвечают те же собственные функции.


 .
. ) сходится еще быстрее при не слишком малых временах t.
) сходится еще быстрее при не слишком малых временах t.







