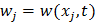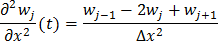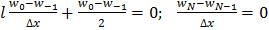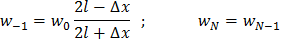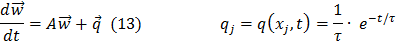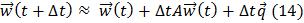Часть 2. Численное решение явным методом Эйлера
Разобьём [0;l] xj=Δx(j+0.5) Δx=l/Nx
Из граничных условий доопределим
Задача 5-6-7 аппроксимируется системой дифференциальных уравнений (13)
Приближенное решение этой системы можно найти явным методом Эйлера, последовательно применяя формулу (14)
Текст программы: #include <math.h> #include <fstream> #include <iostream>
using namespace std;
const double PI=3.1415926535897932384626433832795; const double l=1, tau=1, k=2; double X=2*l/3; double T=k*tau; double D=l*l/tau;
int main() { const int Nx=100; double dx=l/Nx; unsigned int Nt=2000000; double dt=5*tau/Nt; int NT=(int)(k/5*Nt); double a11=-2+(2*l-dx)/(2*l+dx);//элементы матрицы ||А|| double ann=-1;
double u[Nx]; for(int p= 0; p < Nx; p++) { if(((dx*(p+1))<=((17*l)/30))||(((dx*(p+1))>=((23*l)/30)))) u[p]=0; else u[p]=1; }
ofstream out("Tables.txt");//вывод таблиц в файл out<<" "<<"t"<<" "<<"u[2l/3,t]:"<<'\n';//u при фиксированном х double r[Nx];//чтобы задать массив u при t=k*tau
for (int i=0; i<=Nt;i++)//ключевой, шагаем по t { if (i%1000==0) //чтобы в таблице не было слишком много точек out<<dt*i<<" "<<'\t'<<u[(int)(X/l*Nx)]+exp(-(i*dt/tau))-1<<'\n';
double q=exp(-i*dt/tau)/tau; // double v[Nx];//чтобы не портить массив u при решении системы при фиксированном t
v[0]=u[0]+(D*(a11*u[0]-u[1])/(dx*dx)+q)*dt;
for (int j=1;j<Nx-1;j++) { v[j]=u[j]+(D*(u[j-1]-2*u[j]+u[j+1])/(dx*dx)+q)*dt;//система уравнений в явном виде }
v[Nx-1]=u[Nx-1]+(D*(u[Nx-2]+ann*u[Nx-1])/(dx*dx)+q)*dt;
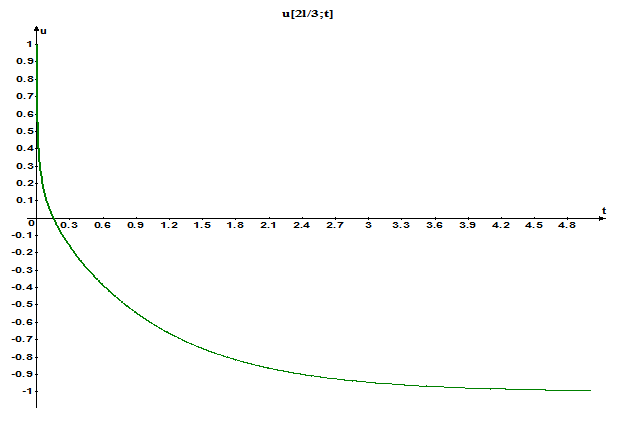
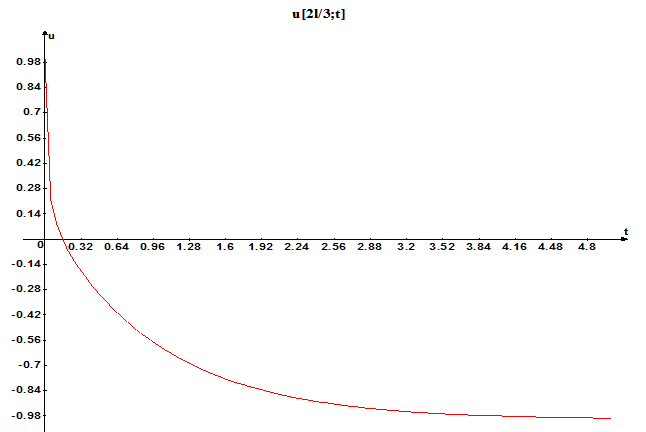
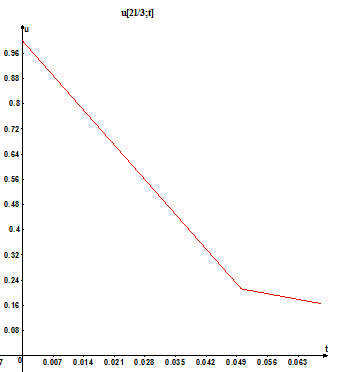
for (int j=1;j<Nx-1;j++) //заход на следующий шаг u[j]=v[j]; if(i==NT) { for (int j=0;j<Nx;j++) //чтобы построить u(x,t*) r[j]=u[j]; } } out<<'\n'<<" "<<"x"<<" "<<"u[x,T]:"<<'\n';//u при фиксированном t for (int j=0;j<Nx-1;j++) out<<(j+0.5)*dx<<" "<<'\t'<<r[j]-(1-exp(-(T/tau)))<<'\n'; return 0; } График при x*=2l/3 Nx=100; Nt=2000000 - количество точек на отрезке [0;τ] (взяли с запасом количество точек разбиения, больше которого изменение графика становится незаметным для данного Nx, то есть для которого явно прослеживается устойчивость решения).
При фиксированном Nx=100 подберем такое количество точек на отрезке [0;τ], что решение начинает терять устойчивость. Мы получили Nt=100000. Отсюда, кстати, можно примерно оценить λmax≈200000 (tau=1). Как можно видеть, на этом этапе график становится негладким.
|

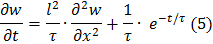
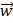 – вектор-столбец, состоящий из
– вектор-столбец, состоящий из