ИТЕРАЦИОННЫЕ ЦИКЛЫ

Такие алгоритмы характеризуются последовательным приближением вычисляемых величин к искомому значению. Окончание цикла в этом случае обычно осуществляется при достижении заданной точности вычисления результата. К итерационным циклам приводят задачи вычисления сумм бесконечных рядов, реализации численных методов решения уравнений, систем уравнений, задачи оптимизации.

Рассмотрим правила составления итерационных циклических алгоритмов на примере вычисления суммы бесконечного ряда. Задача при этом сводится к нахождению с погрешностью, не превышающей , суммы

,

каждое слагаемое которой является функцией номера , а также может являться функцией одного или нескольких дополнительных параметров.

Задача нахождения такой суммы является типичным примером итерационного процесса, так как заранее не известно, при каком номере слагаемого будет достигнута требуемая точность.

Вычисление суммы членов бесконечного ряда возможно лишь в том случае, если получаемая в результате циклического процесса последовательность s(1), s(2), …, s(i), … сходится к своему предельному значению S, т.е. существует предел . Здесь s(i) – сумма i членов бесконечного ряда.

Процесс вычисления суммы членов равномерно сходящегося ряда организуется в виде циклического алгоритма, когда при каждом прохождении цикла номер слагаемого i увеличивается на единицу, а сумма изменяется на величину i-го слагаемого, т.е. , где и 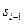- суммы i и i-1 слагаемых. Приведенное выше соотношение в алгоритме вычисления записывается следующим образом: S=S+f(i), что означает добавление слагаемого с номером i к значению суммы, вычисленному на предыдущем шаге алгоритма, и присвоение вычисленного значения S+f(i) той же переменной S. Начальное значение S должно быть равно нулю, в этом случае после первого выполнения цикла значение S будет равно значению первого слагаемого. Суммирование считается законченным при выполнении условия , т.е. если значение очередного вычисленного члена ряда меньше величины погрешности.

Задача 4.